Погода в Санкт-Петербурге | Pogoda78.ru

Разбор задания 15 из ОГЭ (9 класс)материал для подготовки к егэ (гиа) по информатике и икт (9 класс) по теме

Разбор задания 15 из ОГЭ (9 класс)
материал для подготовки к егэ (гиа) по информатике и икт (9 класс) по теме

Материал содержит основную информацию по решению задания 15 из ОГЭ (9 класс).

В материале присутствуют:

• Тип задания;
• Возможные варианты задания;

• Решение с пояснением.

Скачать:

Вложение	Размер
razbor_zadaniya_15_iz_oge.pdf	310.75 КБ

Предварительный просмотр:

Чтобы пользоваться предварительным просмотром создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.com

По теме: методические разработки, презентации и конспекты

Олимпиада по ОПК 2012. Разбор заданий 5-9 классы

Презентация предназначена на вдумчивого анализа заданий олимпиады по основам православной культуры 2012 года, выполненных учащимися 5-9 классов.

Олимпиада по ОПК 2012. Разбор заданий 10-11 классы

Презентация предназначена на анализа заданий олимпиады по основам православной культуры 2012 года, выполненных учащимися 10-11 классов.

Презентация по теме Разбор заданий КИМ ГИА (задание 20.2)

В презентации рассматривается методика выполнения задания 20.2 контрольно-измерительных материалов ГИА. Маиериал можно использовать при подготовке учащихся 9 классов к сдаче экзамена по информатике и .

Разбор задания 1 из ОГЭ (9 класс)

Материал содержит основную информацию по решению задания 1 из ОГЭ (9 класс).В материале присутствуют:Тип задания;Возможные варианты задания;Необходимая информация для решения задания;Решение с пояснен.

Разбор задания 3 из ОГЭ (9 класс)

Материал содержит основную информацию по решению задания 3 из ОГЭ (9 класс).В материале присутствуют:Тип задания;Возможные варианты задания;Решение с пояснением.

Разбор задания 11 из ОГЭ (9 класс)

Материал содержит основную информацию по решению задания 3 из ОГЭ (9 класс).В материале присутствуют:Тип задания;Возможные варианты задания;Решение с пояснением.

ИНФОРМАТИКА . Разбор заданий ОГЭ (Задания 7 и 11)

Разбор заданий поинформатике (Задания 7 и 11)Это анимированный поэтапный разбор заданий,представленный различными спорсобами.

ОРГАНИЗАЦИЯ ДОМАШНЕГО ЗАДАНИЯ ПО ИНФОРМАТИКЕ

Сама проблема организации домашней работы весьма актуальна. Необходимость домашней работы обусловлена не столько решением чисто дидактических задач, сколько задачами формирования навыков самостоятельной деятельности учащихся.

Основное отличие домашней работы от классной заключается в том, что она проходит по указаниям преподавателя, но без его непосредственного участия. Учащийся сам определяет темп и время выполнения работы.

Домашнее задание – это тот же процесс обучения, основанный на познании, но протекающий в новых условиях.

Домашнее задание может быть:

1) средством целесообразной и полезной организации внеучебного времени учащихся;

2) способом приучения детей к систематической самостоятельной интеллектуальной работе;

3) тренингом, способствующим лучшему и прочному запоминанию изучаемого материала;

4) методом воспитания нравственных качеств – трудолюбия, ответственности, чувства долга и пр.;

5) средством обратной связи школы, учителя и родителей ученика и в известной степени воспитания родителей;

6) дополнительным временем к уроку для прохождения и освоения его материала учеником.

Большинство учителей задают домашнее задание в конце урока, но возможны и другие варианты: в начале, в середине и ходе урока.

В связи со спецификой предмета (работа с компьютером) домашнее задание по информатике следует задавать с учетом наличия компьютера у учащихся. Целесообразнее всего задавать такие задания, которые не требуют применения технических средств. Выполнение домашней работы происходит без непосредственного участия учителя, поэтому для ее успешности необходимы определенные условия, одним из них является доступность домашней работы.

Кандидат педагогических наук С.А. Пуйман формулирует основные правила задавания на дом следующим образом:

- для задавания на дом необходимо отводить специальное время;

- давать задание следует при полном внимании всего класса;

- домашнее задание должно быть понятно всем без исключения;

- учащиеся должны знать не только, что делать, но и как делать.

А.А. Гин предлагает целый ряд приемов подачи домашнего задания:

Задание массивом. Например, учитель задает N задач, из которых ученик должен сам выбрать и сделать не менее заранее оговоренного объема заданий.

Особое задание. Хорошо подготовленные школьники могут выполнить более сложное задание.

Творчество работает на будущее. Учащиеся получают и выполняют творческое задание по разработке дидактических материалов, которые могут использоваться учителем в будущем.

Необычная обычность. Учитель задает домашнее задание необычным способом. Например, зашифровав его.

Идеальное задание. Учитель предлагает школьникам выполнить дома работу по их собственному выбору.

Домашнее задание следует дозировать по времени, не допуская перегрузки учащихся, оно должно быть хорошо объяснено и не требовать помощи взрослых.

Большинство слабоуспевающих и даже среднеуспевающих учащихся недобросовестно относятся к выполнению домашних заданий. Одной из причин такого положения является недифференцированность домашних заданий (чаще всего оно общее для всех учащихся класса). Поэтому часто возникает такая ситуация, когда ученику легче переписать домашнюю работу у более сильного учащегося, причем часто это делается наспех, ученик не вникает в суть задания и способ его выполнения.

Необходим дифференцированный подход. Его следует применять на всех этапах обучения не только на уроке, но и при выполнении домашних заданий.

Например, при объяснении темы «Алгоритмизация и программирование» можно использовать двухуровневое домашнее задание.

Первый (базовый) уровень. Обязательный минимум. Задание должно быть понятно и посильно всем ученикам:

Составьте алгоритм решения задачи:

· Дано три числа a,b,c. Найти их сумму и среднее арифметическое.

· Даны катеты прямоугольного треугольника. Найти его гипотенузу и площадь.

Второй (повышенный) уровень. Его задания выполняют ученики, желающие хорошо знать предмет и без особой трудности осваивающие программу. При этом они могут освобождаться от задания первого уровня.

Составьте алгоритм решения задачи:

· Дано три числа a,b,c. Найти сумму и частное двух больших из них.

· По координатам вершин треугольника найти его периметр и площадь.

Дифференцированное домашнее задание особенно важно использовать на этапе закрепления изученного материала. Предлагая дифференцированные домашние задания, следует учитывать:

· способность ребенка к учебной деятельности;

· умение ребенка выражать свои мысли;

· познавательную активность ребенка;

· организованность ребенка в работе.

Дифференцированные домашние задания должны раскрыть перед обучающимися преимущества коллективной деятельности.

Большое внимание на качество выполнения домашнего задания оказывает его проверка. Если проверка домашнего задания производится постоянно, то учащиеся более ответственно подходят к его выполнению и стараются работать дома самостоятельно, чтобы быть готовыми к предстоящему уроку. В связи с этим возникает вопрос об эффективной проверке домашнего задания.

Наиболее традиционными способами проверки домашнего задания являются: устный опрос, письменный опрос, работа с карточками-заданиями. На уроках информатики появляется возможность проверить домашнее задание с помощью компьютерного тестирования.

Формы контроля домашнего задания могут быть различными:

1) контроль письменных домашних заданий во время самостоятельной работы школьников на уроке: формально – у всех, контроль содержания – у отдельных учащихся;

2) контроль устных домашних заданий у отдельных учащихся, в то время как все остальные обсуждают и дополняют ответы товарищей;

3) внеурочная проверка учителем тетрадей; непрямой контроль, основанный на наблюдении за работой ученика на уроке, если предпосылкой для активности школьника являлось выполнение домашнего задания;

4) взаимный контроль учащихся при обмене тетрадями;

5) самоконтроль учащихся: сверка выполненного ими дома с написанным на доске или с воспроизведением с помощью мультимедийного проектора правильным вариантом;

6) контроль письменных работ, который проводится отлично успевающими ребятами;

7) контроль с использованием новых информационных технологий (компьютерные тесты).

Стоит отметить, что проверка домашнего задания обязательно должна сопровождаться оценкой. В случае если ученик получает неудовлетворительную оценку, то ее можно не ставить, а предложить школьнику переделать работу, исправив допущенные ошибки, или дать новое домашнее задание, подобное первому.

Важной педагогической задачей является выбор оптимального объема домашнего задания. Исследованиями установлены нормативы нагрузки домашних заданий.

Если задание является интересным, то время, потраченное на его подготовку, не играет особой роли для школьника. Но, несмотря на это, перед учителем остро стоит проблема ограничения объема домашнего задания, так как перегрузки учащихся не только имеют негативные педагогические последствия, но и могут нанести ущерб здоровью ребенка.

Исходя из всего вышеперечисленного, мы можем выявить ряд требований, предъявляемых к домашним заданиям:

· Систематичность. Необходимо систематически задавать домашнее задание, т.к. задания, которые задаются от случая к случаю, часто не выполняются учащимися.

· Обязательность выполнения и проверки домашнего задания.

· Посильность домашнего задания. Задания, которые ученик получает на дом, должны быть легче или равны по сложности заданиям, которые решаются в классе.

· Дифференциация домашнего задания.

· Правильность объема домашнего задания.

· Взаимосвязь классной и домашней работы.

Без тщательно продуманной, регулярно и систематически выполняемой домашней работы невозможно достичь высокого качества обучения. Домашние задания развивают у учащихся познавательный интерес и умение работать самостоятельно.

Внеклассная работа

1. Сущность внеклассной работы её функции.

2. Содержание ВР

3. Формы и средства ВР

4. Особенности организации ВР по информатике

Сущность внеклассной работы её функции.

Внеклассная работа является одним из важных средств развития личности школьника, поэтому тема «Внеклассная работа по информатике» имеет большое значение для профессиональной подготовки будущего учителя информатики.

Педагогическая профессия требует постоянного творческого поиска, самосовершенствования, повышения профессионального уровня. В наибольшей степени это касается учителя информатики вследствие непрерывного изменения содержания и целей обучения, возрастания уровня компьютерной грамотности учащихся. Поэтому учитель информатики должен непрерывно следить за публикациями в периодической печати (журналы «Информатика и образование», «Компьютер в школе», «Компьютерные инструменты в образовании» и т.п., газета «Информатика», другие издания компьютерной тематики). Мы надеемся, что в скором времени для активизации внеклассной работы учителя смогут воспользоваться новыми возможностями и информационными ресурсами, предоставляемыми сетью Интернет.

Задача учителя - развернуть перед взором учащихся спектр разнообразных видов деятельности, отвечающих их интересам и возможностям, поощрять самостоятельные поиски и творчество. Ученик должен иметь право выбора, самоутверждения, показать свою индивидуальность. Учитель должен помочь ему осознать свои способности, увлечь и поддержать.

Требования, предъявляемые программой по информатике школьными учебниками и сложившейся методикой обучения, рассчитаны на «среднего» ученика. Однако имеет место резкое расслоение учащихся: на тех, кто легко и с интересом усваивают программный материал по информатике, на тех, кто добивается при изучении информатики лишь удовлетворительных результатов, и тех, кому успешное изучение информатики дается с большим трудом.

Все это приводит к необходимости индивидуализации обучения информатике, одной из форм которой является внеклассная работа.

Внеклассная работа - различные воспитательно-образовательные мероприятия, выходящие за рамки обязательных учебных программ и проводимые школой во вне­урочное время.

Цель и задачи внеклассной работы

Являясь составной частью воспитательной работы в школе, внеклассная работа направлена на достижение общей цели обучения и воспитания - усвоения ребенком необходимого для жизни в обществе социального опыта и формирования принимаемой обществом системы цен­ностей.

Внеклассная работа направлена на решение следующих задач:

1. Формирование у ребенка положительной Я-концепцгш, характеризующейся следующими факторами: а) уверенностью в доброжелательном отношения к нему других людей; б) убежденностью в успешном овладении им тем или иным видом деятельности; в) чувством собственной значимости. Положительная Я-концепция характеризует позитивное отношение ребенка к самому себе и объективность его самооценки, которая является основой дальнейшего развития индивидуальности ребенка.

Разнообразная внеклассная деятельность способствует раскрытию индивидуальных способностей ребенка, которые не всегда проявляются на уроке. Разнообразие внеклассной деятельности способствует самореализации ребенка, повышению его самооценки, уверенности в себе, т.е. положительному восприятию самого себя. Включение учащихся в различные виды внеклассной работы обогащает их личный опыт, знания о разнообразии человеческой деятель­ности, формирует необходимые практические умения и навыки.

2. Создание благоприятных условий для накопления опыта коллективной жизни, навыков сотрудничества. Учебный труд в силу его специфичности не может служить такой благоприятной основой сплочения коллектива, какой является внеклассная деятельность. Здесь учащиеся вступают в многосторонние взаимоотношения между собой.

В различных формах внеклассной работы учащиеся не только проявляют свои индивидуальные особенности, но и учатся жить в коллективе. При этом внеклассная деятельность обогащает опыт коллективного взаимодействия школьников в определенном аспекте, что в своей совокупности дает большой учебно-воспитательный эффект.

3. Формирование потребности в продуктивной, социально-одобряемой деятельности через непосредственное знакомство с различными видами деятельности, формирование в соответствии с индивидуальными наклонностями интереса к ним, необходимых умений и навыков. Во внеклассной работе создаются условия для формирования умений включаться в продуктивную, одобряемую обществом деятельность и при необходимости самостоятельно ее организовывать. Этот момент особенно актуален в связи с ростом количества подростков, ведущих антиобщественный образ жизни (преступность, наркомания, алкоголизм и т.п.).

4. Формирование нравственного, эмоционального, волевого компонентов мировоззрения. Во внеклассной работе усваиваются моральные нормы поведения через овладение нравственными понятиями. Эмоциональная сфера формируется через эстетические представления в творческой деятельности.

5. Развитие познавательного интереса. Данная задача внеклассной работы отражает преемственность учебной и внеучебной деятельности, так как внеклассная работа связана с учебно-воспитательной работой на уроке и, в конечном счете, направлена на повышение эффективности учебного процесса.

Воспитание интересов учащихся в процессе внеклассной работы связано с решением важной задачи - выбором школьниками профессии и подготовкой их к труду. Известно, что различные виды внеклассных занятий являются одним из основных источников возникновения профессиональных интересов и профессиональной осведомленности учащихся, помогают им приобрести специальные знания, умения и навыки, проверить свои силы в избранной области деятельности.

6. Организация свободного времени учащихся. В настоящее время очень важно удлинить сроки организованного педагогического влияния, чтобы предупредить отрицательные последствия детской безнадзорности.

Установлена зависимость между поведением учащихся и тем, как они проводят свободное время. Педагогически запущенные учащиеся в большинстве своем не занимаются в кружках, не имеют общественных поручений, не интересуются жизнью класса и школы. По мере увеличения свободного времени проблема культуры его использования приобретает все большее значение в обществе.

Существует мнение, что неуспевающих учеников не следует отвлекать от учебных занятий. Это неверно, так как именно им надо помочь правильно использовать свое свободное вре­мя. Информатика предоставляет огромные возможности и для слабоуспевающих учащихся.

Перечисленные задачи определяют основные возможности и направления внеклассной работы в достижении ее основной цели и носят характер общих положений. В реальной воспитательной работе они конкретизируются в соответствии с особенностями класса, самого педагога, с общешкольной внеучебной работой и т.д.

Функции внеклассной работа

Цель и задачи внеклассной работы определяют ее функции - обучающую, воспитатель­ную и развивающую.

Обучающая функция внеклассной работы не имеет такого приоритета, как в учебной дея­тельности. Во внеклассной работе она является вспомогательной для более эффективной реали­зации воспитательной и развивающей функций и заключается не в формировании системы научных знаний, учебных умений и навыков, а в обучении определенным навыкам поведения, коллективной жизни, навыкам общения и пр.

Однако правильное сочетание внеклассной и учебной работы обеспечивает большую гибкость всей системы учебно-воспитательной деятельности. Внеклассная работа может служить эффективным средством дифференциации обучения и воспитания при сохранении единого и обязательного учебного плана. Внеклассная работа может компенсировать его недостатки, трудно устранимые в рамках учебной деятельности из-за ее большой насыщенности обязательными занятиями.

Огромное значение во внеклассной работе имеет развивающая функция, которая заключается в выявлении и развитии индивидуальных способностей, склонностей и интересов учащихся через включение их в соответствующую деятельность. Например, ученика с артистиче­скими способностями можно привлечь к участию в школьных праздниках, КВН и т.д., со способностями к информатике - к участию в олимпиаде, разработке полезных программ, составлении дидактических материалов и т.д.

Воспитательная функция нашла своё выражение через воспитание культуры жизни в коллективе.

Решение 15 задания ЕГЭ по информатике про основные законы Алгебры Логики

15-е задание: «Основные законы алгебры логики»
Уровень сложности — повышенный,
Требуется использование специализированного программного обеспечения — нет,
Максимальный балл — 1,
Примерное время выполнения — 5 минут.

Проверяемые элементы содержания: Знание основных понятий и законов математической логики

"Важно понимать, что выражение должно быть тождественно истинно, т.е. истинно при любых допустимых значениях переменных x и у, а не только при некоторых наборах значений"

Элементы математической логики

Для решения 15 задания, потребуется знание таблиц истинности.

Для выполнения задания рекомендуется повторить следующие темы:

1. выражения в скобках,
2. операции «НЕ»,
3. операции «И»,
4. операции «ИЛИ»,
5. операции «импликация»
6. операции «эквиваленция»

Математическая логика и теория множеств

• пересечение множеств соответствует логическому умножению, а объединение – логическому сложению;
• пересечением двух множеств называется новое множество, состоящее из элементов, принадлежащих одновременно обеим множествам:

Пример: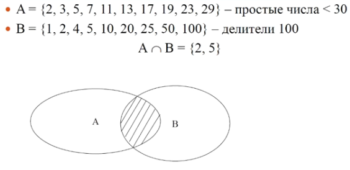

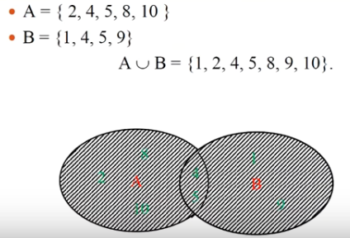
Пример:

Пример разности множеств: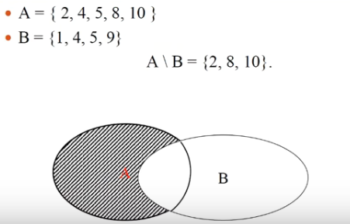

Для большей определенности стоит рассмотреть тему круги Эйлера

Задания с отрезками и ДЕЛ

Для решения заданий необходимо знать рассмотренную тему о множествах.

Для упрощения решений можно пользоваться следующими законами.

1. Если в задании формула тождественно истинна (равна 1), и
2. после упрощения A без отрицания
то используется закон:

где B — известная часть выражения.

1. Если в задании формула тождественно истинна (равна 1), и
2. после упрощения A с отрицанием
то используется закон:

где B — известная часть выражения.

1. Если в задании формула тождественно ложна (равна 0), и
2. после упрощения A без отрицания
то используется закон:

где B — известная часть выражения.

1. Если в задании формула тождественно ложна (равна 0), и
2. после упрощения A с отрицанием
то используется закон:

Задания с поразрядной конъюнкцией

В задании 15 ЕГЭ встречаются задачи, связанные с поразрядной конъюнкцией.
Например:

означает поразрядную конъюнкцию (логическое «И») между двоичными значениями двух чисел — 5 и 26. Выполняется так:

Задания, связанные с поразрядной конъюнкцией, решаются несколькими способами. Рассмотрим один из них.

• Обозначим:
• Для решения методом, предложенным А.В. Здвижковой, пригодится использование следующих свойств:

• На деле, это означает, что если имеем:
• то сначала введем замену:
• а затем, используя свойство 3, определим истинность высказывания Z₂₉ → Z₅:
• таким образом, получили:

• Так, например, если в задании имеем:
• то сначала введем замену и, используя свойство 4, получим:

Решение заданий 15 ЕГЭ по информатике

Плейлист видеоразборов задания на YouTube:

Задания с множествами

Элементами множества А являются натуральные числа. Известно, что выражение

истинно (т. е. принимает значение 1) при любом значении переменной х .

Определите наименьшее возможное значение суммы элементов множества A .

• Введем обозначения:
• Выполним преобразования:
• Разделим выражение на две части — известную часть и неизвестную. Чтобы неизвестная часть ( А ) была непременно истинной, необходимо, чтобы известная часть была ложна:
• То есть получаем:
• Таким образом имеем пересечение (умножение) двух множеств Q и P . То есть необходимо выбрать элементы, которые встречаются в обоих множествах одновременно:
• Сумма элементов:

Ответ: 12

Элементами множества А являются натуральные числа. Известно, что выражение

истинно (т. е. принимает значение 1) при любом значении переменной х .

Определите наименьшее возможное значение суммы элементов множества A .

• Введем обозначения:
• Выполним преобразования:
• Разделим выражение на две части — известную часть и неизвестную. Чтобы неизвестная часть ( А ) была непременно истинной, необходимо, чтобы известная часть была ложна:
• То есть получаем:
• Таким образом имеем пересечение (умножение) двух множеств Q и P . То есть необходимо выбрать элементы, которые встречаются в обоих множествах одновременно:
• Сумма элементов:

Ответ: 18

Элементами множеств А , P , Q являются натуральные числа, причём P = <2, 4, 6, 8, 10, 12, 14, 16, 18, 20>, Q = <3, 6, 9, 12, 15, 18, 21, 24, 27, 30>. Известно, что выражение

истинно (т. е. принимает значение 1) при любом значении переменной х .

Определите наибольшее возможное количество элементов в множестве A .

• Введем обозначения:
• Выполним преобразования:
• Разделим выражение на две части — известную часть и неизвестную. Чтобы неизвестная часть ( А ) была непременно истинной, необходимо, чтобы известная часть была ложна:
• То есть получаем:
• Таким образом имеем разность двух множеств Q и P . То есть это новое множество, элементы которого принадлежат P , но не принадлежат Q :
• Количество элементов = 7

Ответ: 7

Элементами множества А являются натуральные числа. Известно, что выражение

истинно (т. е. принимает значение 1) при любом значении переменной х .

Определите наименьшее возможное количество элементов множества A.

• Введем обозначения:
• Выполним преобразования:
• Разделим выражение на две части — известную часть и неизвестную. Чтобы неизвестная часть ( А ) была непременно истинной, необходимо, чтобы известная часть была ложна:
• То есть получаем:
• Таким образом имеем пересечение двух множеств Q и P :
• Количество элементов = 1

Ответ: 1

Задания с отрезками на числовой прямой

Отрезки на числовой прямой:

На числовой прямой даны два отрезка: P=[44,48] и Q=[23,35].

Укажите наибольшую возможную длину отрезка А, для которого формула

тождественно ложна, то есть принимает значение 0 при любом значении переменной x.

✍ Решение:

• Упростим формулу, избавившись от ‘x ϵ‘:
• Теперь преобразуем импликацию в скобках:

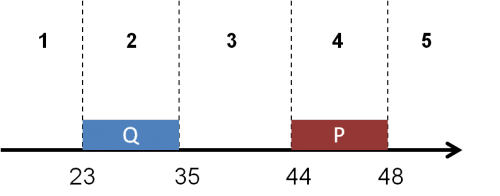
Результат: 4
✎ Решение 2 (программирование):
Внимание! этот способ подходит НЕ для всех заданий с отрезками!
Python:

def f(a1,a2,x): return((44<=x<=48)<=(23<=x<=35))and(a1<=x<=a2) maxim = 0 for a1 in range (1,200): for a2 in range (a1+1,200): if all(f(a1,a2,x)==0 for x in range (1,200)):# если все ложны if a2-a1>maxim: maxim=a2-a1 print(a1,a2, a2-a1) # сами точки отрезка и длина

PascalABC.net:

С подробным решением задания 15 ЕГЭ по информатике можно ознакомиться по видео:

Отрезки на числовой прямой:

На числовой прямой даны два отрезка: P = [10,20] и Q = [30,40].

Укажите наибольшую возможную длину отрезка A, для которого формула

тождественно истинна, то есть принимает значение 1 при любом значении переменной x.

✍ Решение:

• Упростим выражение, введя обозначения:
• Запишем формулу с новыми обозначениями, учитывая, что по условию она должна быть тождественно истинной:
• Избавимся от импликации:
• Используем закон Де Моргана для последующего преобразования:
• А — наше неизвестное, а выделенную часть формулы можно найти. Необходимо, чтобы А = 1. Значит, предположим, что ¬А = 0, тогда P ∧ ¬Q = 1 (если P ∧ ¬Q = 0, то ¬А может равняться и 0 и 1, так как имеет место операция логического сложения ∨)
• Значит, имеем P ∧ ¬Q = 1. Кроме того, в данном случае имеет место операция конъюнкция, которую проще вычислить, если выражение равно 1 (так как для конъюнкции существует один единственный случай истинности: 1 & 1 = 1). Таким образом имеем утверждения:
• Т.е. A истинно (=1) на промежутке пересечения отрезков P и ¬Q.
• Отобразим отрезки на числовой прямой, чтобы найти искомое значение:

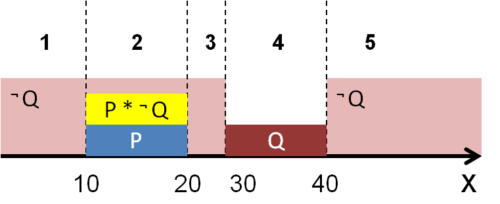
Результат: 10

Отрезки на числовой прямой:

На числовой прямой даны два отрезка: P = [3, 20] и Q = [6, 12].

Укажите наибольшую возможную длину отрезка A, для которого формула

тождественно истинна, то есть принимает значение 1 при любом значении переменной x.

✍ Решение:

• Упростим выражение, введя обозначения:
• Запишем формулу с новыми обозначениями, учитывая, что по условию она должна быть тождественно истинной:
• Избавимся от импликации:

Далее возможно 2 способа решения.

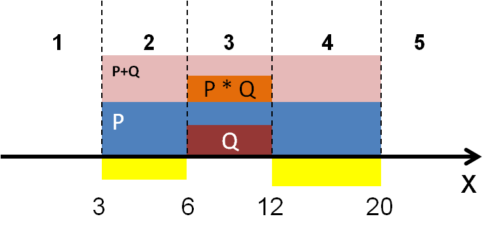
✎ 2 способ:
После того, как мы избавились от импликации, имеем:

Результат: 8

С решением задания 15 вы также можете ознакомиться, посмотрев видео:

Отрезки на числовой прямой:

На числовой прямой даны два отрезка: P = [11, 21] и Q = [15, 40].

Укажите наибольшую возможную длину отрезка A, для которого формула

тождественно истинна, то есть принимает значение 1 при любом значении переменной x.

✍ Решение:

• Упростим выражение, введя обозначения:
• Запишем формулу с новыми обозначениями, учитывая, что по условию она должна быть тождественно истинной:
• Избавимся от импликации:
• А — наше неизвестное, тогда как выделенную часть формулы можно найти. Введем предположение, что А = 1. Значит, ¬А = 0 (т.е. А = 1), тогда ¬(P

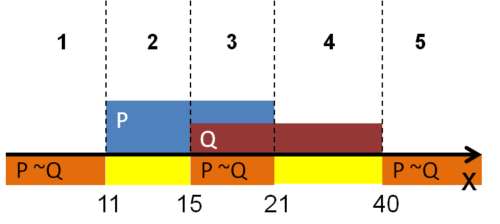
Результат: 19

Задания с ДЕЛ

Поиск наибольшего А, известная часть Дел ∨ Дел = 1

Для какого наибольшего натурального числа А формула

тождественно истинна (то есть принимает значение 1 при любом натуральном значении переменной х)?

✍ Решение:

• Введем обозначения:
• Перепишем исходную формулу, согласно введенным обозначениям. Укажем, что формула должна быть тождественно истинна (по условию):
• Избавимся от импликации:
• Разделим данную формулу на две части: в одной из них — искомое A, а в другой — часть формулы с x, которую можно найти:
• В полученной формуле необходимо, чтобы искомая часть с A в конечном счете было истинно.

Далее можно решать задание либо с помощью кругов Эйлера, либо с помощью логических рассуждений.

Решение с помощью логических рассуждений:

Решение с помощью кругов Эйлера:

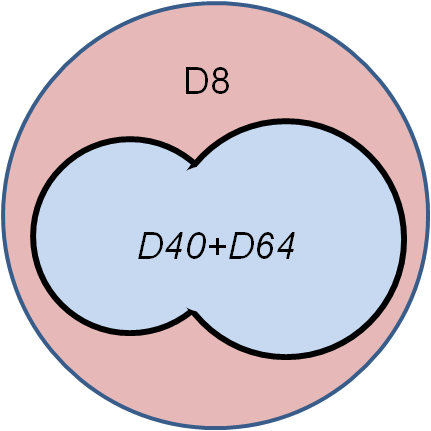
Результат: 8

✎ Решение 2 (программирование):
Python:

for A in range(1,500): OK = 1 for x in range(1,1000): OK *= ((x % 40 == 0) or (x % 64 == 0))<=(x % A== 0) if OK: print( A )

PascalABC.net:

begin for var A := 1 to 500 do begin var ok := 1; for var x := 1 to 1000 do begin if (((x mod 40 = 0) or (x mod 64 = 0)) <= (x mod A = 0)) = false then begin ok := 0; break; end; end; if (ok = 1) then print(A) end; end.

Результат: 8

Поиск наименьшего А, известная часть Дел ∧ ¬Дел = 1

Для какого наименьшего натурального числа А формула

тождественно истинна (то есть принимает значение 1 при любом натуральном значении переменной х)?

✍ Решение:

Избавимся от импликации:

✎ Решение 2 (программирование). Язык Python, Pascal:

Из общего выражения:

for A in range(1,50): OK = 1 for x in range(1,1000): OK *= (x % A == 0) <= ((x % 28 != 0) or (x % 42== 0)) if OK: print( A ) break

begin for var A := 1 to 50 do begin var ok := 1; for var x := 1 to 1000 do begin if (x mod A = 0) <= ((x mod 28 <> 0)or (x mod 42 = 0)) = false then begin ok := 0; break; end; end; if (ok = 1) then begin print(A); break; end end; end.

Результат: 3

Для какого наименьшего натурального числа А формула

тождественно истинна (то есть принимает значение 1 при любом натуральном значении переменной х)?

✍ Решение:

• Введем обозначения:
• Перепишем исходную формулу, согласно введенным обозначениям. Укажем, что формула должна быть тождественно истинна (по условию):
• Избавимся от импликации:
• Разделим данную формулу на две части: в одной из них - искомое A, а в другой - часть формулы с x, которую можно найти:

✎ Решение 2 (программирование). Язык Python:

Из общего выражения:

for A in range(1,500): OK = 1 for x in range(1,1000): OK *= ((x % 19 != 0) or (x % 15 != 0))<= (x % A!= 0) if OK: print( A )

Результат: 285

Задания с поразрядной конъюнкцией

Для какого наименьшего неотрицательного целого числа A формула

тождественно ложна (то есть принимает значение 0 при любом неотрицательном значении переменной X)?

✍ Решение:

• Удалим из формулы X&, чтобы сократить ее запись:
• Обратим внимание, что внешней операцией является конъюнкция - логическое умножение:
• Разделим общее выражение на две части относительно внешней операции. Первая часть - неизвестная, искомая, а вторая - известная, ее можно вычислить:
• Выполним некоторые преобразования во второй части формулы:
• Зная свойство импликации, преобразуем формулу (избавимся от импликации в скобках):

Ответ: 3

Используем метод А.В. Здвижковой.

1. Произвести замену (x & K = 0) на Zk
2. Выполнить преобразования по свойству импликации и закону Де Моргана.
3. Стремиться прийти к выражению с конъюнкциями без отрицаний типа: Zk * Zm .
4. Все выражения типа Zk * Zm преобразовать по свойству
   Zk * Zm = Z_{k or m} .
5. Путем преобразований прийти к импликации: Zk → Zm .

Условие Zk → Zm истинно для любых натуральных значений x тогда и только тогда, когда все единичные биты двоичной записи числа M входят во множество единичных битов двоичной записи числа K.

Результат: 3

Детальный разбор данного задания 15 ЕГЭ по информатике предлагаем посмотреть на видео:

Вариант решения №1 (универсальный):

Вариант решения №2 (не универсальный, но простой):

Для какого наибольшего неотрицательного целого числа A формула

тождественно истинна (то есть принимает значение 1 при любом неотрицательном значении переменной X)?

✍ Решение:

Результат: 38

Подробное решение данного задания 15 ЕГЭ по информатике предлагаем посмотреть в видео уроке:
Способ 1:

Определите наименьшее натуральное число А из интервала [43, 55], такое, что выражение

тождественно ложно (то есть принимает значение 0 при любом натуральном значении переменной х)?

✍ Решение:

Кратко изложенное решение *:

Результат: 48

Определите набольшее натуральное число A, такое что выражение

тождественно истинно (то есть принимает значение 1 при любом натуральном значении переменной х)?

✍ Решение:

• Для упрощения восприятия введем обозначения:
• Таким образом, получим следующее выражение:
• Упростим выражение по свойству импликации для второй скобки:
• Упростим левую часть, используя свойство 2 ( Z_k + Z_m = Z_{k and m} ):
• То есть получили z26 ∨ z13 = z8
• По правилу импликации: все единичные биты двоичной записи результата (z78 ∨ A) должны входить во множество единичных битов двоичной записи z8.
• Рассмотрим:
• Для А единичными битами должны быть общие единичные биты для z8 (1000₂). Т.е. в нашим случае - это один бит - 3-й:

Результат: 8

Задания на поиск наибольшего или наименьшего числа А

Поиск наибольшего или наименьшего числа А:

Для какого наибольшего целого числа А формула
alt="демоверсия егэ 2018 решение 15 (18) задания" width="500" height="42" />
тождественно истинна, то есть принимает значение 1 при любых целых неотрицательных x и y?

begin for var A := 200 downto -100 do begin var OK := 1; for var x := 0 to 100 do for var y := 0 to 100 do if ((x <= 9) <= (x * x <= A)) and ((y * y <= A) <= (y <= 9)) = false then begin OK := 0; break; end; if OK = 1 then begin print(A); break end; end; end.

for A in range(200,-100,-1): OK = 1 for x in range(0,100): for y in range(0,100): OK *= ((x<=9) <= (x*x<=A)) and((y*y<=A) <= (y<=9)) if OK: print(A) break

✎ Способ 2 (теоретическое решение):

Условно разделим исходное выражение на части:

(импликация 0 → 0 = 1)

Результат: 99

Подробное решение 15 (18) задания демоверсии ЕГЭ 2018 года смотрите на видео:

Поиск наибольшего или наименьшего числа А:

Укажите наименьшее значение А, при котором выражение

истинно для любых целых положительных значений x и y.

✍ Решение:

begin for var A := -100 to 200 do begin var OK := 1; for var x := 1 to 100 do for var y := 1 to 100 do if ((y+3*x<A) or (x >20)or(y>40)) = false then begin OK := 0; break; end; if OK = 1 then begin print(A); break end; end; end.

for A in range(-100,200): OK = 1 for x in range(1,100): for y in range(1,100): OK *= (y+3*x<A) or (x > 20) or (y > 40) if OK: print(A) break

✎ Способ 2 (теоретическое решение):

• Определим основные части выражения, выделив отдельно неизвестную часть - с А, и, так сказать, известную часть, то есть остальную.
• Поскольку основными операциями являются операции дизъюнкции (логического сложения) и порядок их выполнения не важен, то последней, внешней, операцией будем выполнять дизъюнкцию слева, т.к. она объединяет неизвестную и известную часть.
• Сначала важно рассмотреть вторую часть выражения, известную, так как от нее будет зависеть значение A. Если вторая часть истинна, то А может быть как = 1, так и = 0. Такой вариант нам не подходит:
• Соответственно, рассмотрим вариант, когда вторая часть ложна, тогда часть выражения с неизвестным А будет обязательно истинной, т.е.:
• Дизъюнкция ложна, когда оба операнда ложны, т.е. из второго пункта имеем:
• Для того, чтобы перекрыть все x и все y, возьмем наибольшие из возможных значений: x = 20, y = 40.
• Выразим А:
• Поскольку требуется найти наименьшее значение А, то имеем А = 101 .

Результат: 101

Подробное решение досрочного ЕГЭ 2018 года смотрите на видео:

Поиск наибольшего или наименьшего числа А:

Для какого наибольшего целого неотрицательного числа А выражение

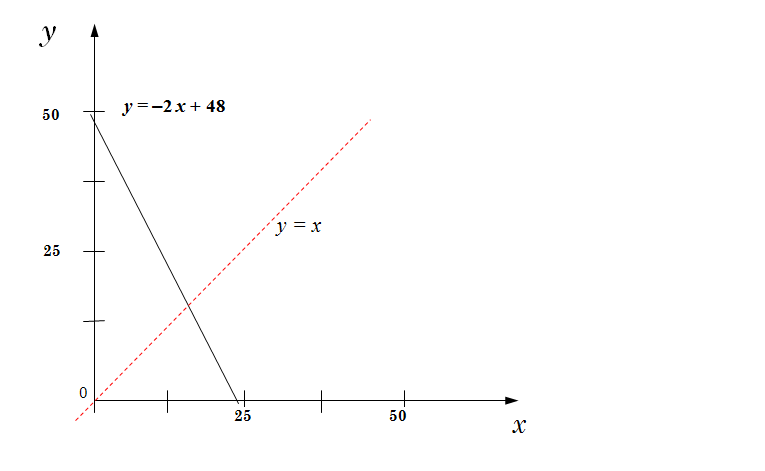
✎ Решение 2 (программное):
Python:

for A in range(200,0,-1): OK = 1 for x in range(0,100): for y in range(0,100): OK *= (48!=y+2*x) or(A<x)or (A<y) if OK: print(A) break

Результат: 15

Видео решения 15 (18) задания демоверсии ЕГЭ 2019:

Поиск наибольшего или наименьшего числа А:

Для какого наименьшего целого числа А формула

✎ Решение 2 (программное):
Python:

for A in range(-100,100): OK = 1 for x in range(0,100): for y in range(0,100): OK *= (y+5*x<=34)<=((y-x >4)or(y<=A)) if OK: print( A ) break

begin for var A := -100 to 100 do begin var OK := true; for var x := 0 to 100 do begin for var y := 0 to 100 do begin OK := (y + 5 * x <= 34) <= ((y - x > 4) or (y <= A)); if OK = false then break; end; if OK = false then break; end; if OK then begin print(A); break; end; end; end.

Результат: 9

Поиск наибольшего или наименьшего числа А:

Укажите наименьшее целое значение А при котором выражение

(2y + 5x 100) ∨ (3x – 2y > 70)

истинно для любых целых положительных значений x и y.

for A in range(-200,200): OK = 1 for x in range(1,100): for y in range(1,100): OK *= (2*y + 5*x < A) or (2*x + 4*y > 100) or (3*x - 2*y > 70) if OK: print( A ) break

begin for var A := -200 to 200 do begin var OK := true; for var x := 1 to 100 do begin for var y := 1 to 100 do begin OK := (2*y + 5*x < A) or (2*x + 4*y > 100) or (3*x - 2*y > 70); if OK = false then break; end; if OK = false then break; end; if OK then begin print(A); break; end; end; end.

Результат: 171

Видео разбора задания смотрите на видео:

Поиск наибольшего или наименьшего числа А:

Укажите наибольшее целое значение А при котором выражение

(3y – x > A) ∨ (2x + 3y ✎ Решение 1 (теоретическое):

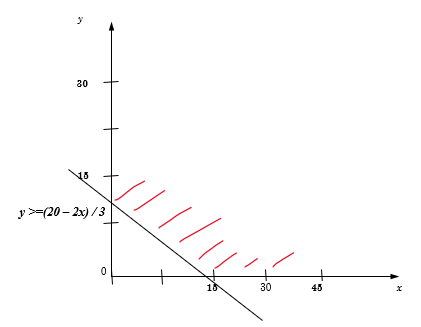
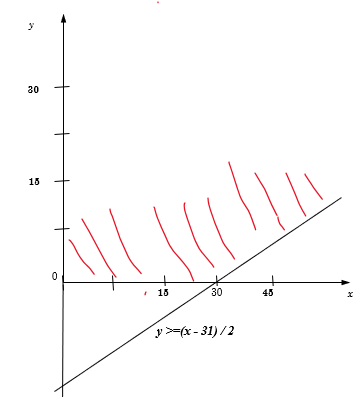
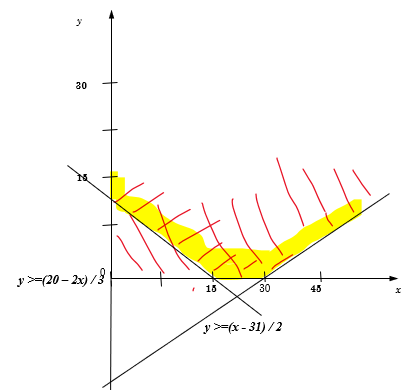
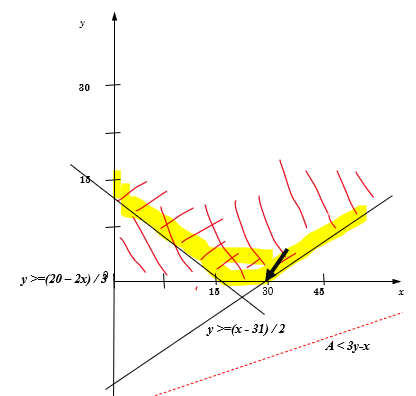
for A in range(200,-200,-1): OK = 1 for x in range(1,100): for y in range(1,100): OK *= (3*y-x>A) or (2*x+3*y<30) or (2*y-x<-31) if OK: print(A) break

Результат: -31

Смотрите решение подобного задания № 296 (К. Поляков):

Рубрики:

Спасибо. Все понятно!

Светлана

Noname

Почему в первой задаче длина отрезка 4,если в отрезок входят: 44,45,46,47,48. Т.е. пять цифр.

Игорь

я думал, что я один такой умный. Замечание правильное. Ответ = 5 .
Потому что в задании сказано промежуток, а не отрезок. Крылов с Чуркиной тоже ошиблись ��
Промежуток (математика)
Промежуток, или более точно, промежуток числовой прямой — множество вещественных чисел, обладающее тем свойством, что вместе с любыми двумя числами содержит любое, лежащее между ними.
В задаче имеется в виду конечно же промежуток не вещественных, а целых чисел.

admin

Спасибо) значит, исправим само задание: вместо «промежуток» укажем «отрезок»

Аноним

18_10 видео не соответствует задаче.

Аноним

Галина

26 в 10-ой =11010 в 2-ой
А в целом большое спасибо!

admin

Аноним

Последняя задача (18_14.) не соответствует задаче в прикреплённом видеоролике, но ответ указан от задания в видео. Можно узнать правильный ответ?

admin

Там написано, что в видео объясняется подобное задание № 296 К. Полякова

Алекс

Простите, я не понимаю…
В примере 130&x=3.
130=10000010.
Побитовая конъюнкция с каким числом даст 3.
10000010 & xxxxxxxx =00000011
Поразрядная конъюнкция с последним 0 всегда даст 0, то есть такого числа не существует.
Или я чего-то не понимаю.

admin

каждый бит одного числа умножить на соответствующий ему бит другого числа — это поразрядная конъюнкция

Полина

Добрый день!
Разбираю теорию, исследую первое свойство поразрядной конъюкции. В нем Z(k) * Z(n) = Z(k or n), и здесь необходимо применять поразрядую дизъюнкцию. Обнаружила ошибку: 26 и 5 дадут 31, но в разобранном примере ответ равен 29. А все дело в том, что неверно представлено число 26 в 2 СС. Оно равно не 11000, а 11010.
Прошу исправить ошибку, иначе школьники совсем запутаются!
Спасибо)

admin

Спасибо большое! исправлено)

Виталий

В связи со свойством 4 у вас пара ошибок:
1) У вас написано, что свойство верно для выражения x & 125 = 5, а применяете вы его к выражению X & 130 = 3, для которого неизвестно ещё ничего о его верности.
2) В первом же шаге, у вас «замена» X & 130 = 3 на Z_130 = 3, но проведя обратную замену по определению над свойством 1, получим 3 = Z_130 = ( x & 130 = 1) — тождественно ложное утверждение в множестве натуральных чисел, т.к. 1 не равно 3 в множестве целых.

И вообще, всем было бы проще и понятнее, если бы вы по-разному обозначали операции в булевой алгебре множеств (\cap, \cup), в кольце целых чисел (+, \times) и логические операции (логическое «или», логическое «и»). Вообще круто было бы ещё и нейтральные элементы обозначать по-разному, хотя бы для булевой алгебры множеств и всего остального.