Погода в Санкт-Петербурге | Pogoda78.ru

Решение задач по сопромату на заказ

Решение задач по сопромату на заказ

Мы коллектив авторов учебных работ. У нас вы можете заказать решение задач по сопромату или любую учебную работу без посредников и переплат. Для оформления заявки выберите тип работы, предмет и тему, при необходимости приложите методичку или другие дополнительные материалы.

Заполните форму ниже и мы ответим Вам в течение 10 минут!

Сопротивление материалов – предмет, который часто ставит студентов в тупик. Поэтому многих выручает такая услуга, как решение задач по сопромату на заказ, позволяющая сэкономить нервы и драгоценное время. На нашем сайте вы сможете получить качественное решение быстро и за доступную цену. У нас работают опытные толковые специалисты, свободно владеющие данной дисциплиной.

Где заказать решение задач по сопромату

В современном мире при наличии интернета можно легко купить решение задач по сопротивлению материалов, потратив на это лишь пару минут своего времени. Но не нужно забывать, что на просторах сети много мошенников, стремящихся завладеть вашими кровными. Часто воспользовавшись услугами непрофессионала, студенты получают низкий балл за свое задание. Поэтому нужно стремиться к тому, чтобы решение задач по сопромату на заказ выполнялось грамотным специалистом, разбирающимся в специфике данной дисциплины. Найти такого исполнителя вы сможете у нас на сайте.

Мы предоставляем студентам услуги по выполнению разнообразных учебных заданий. Здесь можно заказать решение задач по сопромату по любой тематике:

• Растяжение и сжатие
• Срез и смятие
• Закон Гука
• Кручение
• Изгиб
• Построение эпюр

За какое бы задание не взялись наши специалисты, они выполнят его безупречно. Чтобы купить решение задач по сопромату, заполните несложную форму заявки на нашем сайте. Далее с вами в течение получаса свяжется наш консультант. Ему можно будет задать вопросы, касающиеся условий заказа. Также вы сможете уточнить, сколько стоит решение задач по сопротивлению материалов. Если цены и условия вас устроят, то вы сможете внести предоплату и подтвердить свой заказ. Готовое задание будет предоставлено вам в оговоренные сроки.

Оптимальное сочетание качества и цены

Каждого учащегося, собирающегося заказать решение задач по сопромату, интересует, во сколько ему это обойдется. У студента нет достаточно средств, чтобы оплачивать слишком дорогие услуги. Поэтому часто они готовы экономить на качестве работы, лишь бы она обошлась дешево. У нас не придется делать такого выбора. Здесь вы получаете решение задач по сопромату недорого, при этом выполнено оно будет с высоким уровнем грамотности. К своей работе мы относимся с максимальной ответственностью, для нас важен каждый клиент. Заказав работу у нас, вы сможете сдать ее с высоким баллом.

Примеры решения задач по сопромату

Приветствую тебя, читатель сайта — sopromats.ru, на котором размещено много полезной и интересной информации о сопромате и не только. Сегодня я решил написать большую статью о примерах решения задач по сопромату, которые размещены на этом ресурсе. Все примеры было решено классифицировать на три категории: по виду деформации, по виду рассчитываемого объекта и по типу расчета. Эти категории имеют три уровня вложенности. Например, в категории — по виду деформации входят задачи, связанные с изгибом, кручением, растяжением (сжатием) и сложным сопротивлением. В свою очередь, решения на изгиб классифицируются на статически определимые и неопределимые. Для того, чтобы найти нужную категорию перемещайтесь по указанным ссылкам на страничках. Также хотелось бы отметить, что на данный момент на сайте преобладают рукописные примеры решения. Но наша команда, активно работает над добавлением электронных материалов: с качественными схемами и набранными в цифровом виде расчетами. По мере развития сайта, все рукописные записи, планируется заменить цифровыми. Ну что же перейдем непосредственно к нашим примерам.

Классификация по виду деформации

Как уже говорилось выше, здесь все примеры отсортированы по виду деформации: растяжению и сжатию, кручению, изгибу и сложному сопротивлению. В категорию задач на сложное сопротивление попадают такие популярные решения на такие темы как изгиб с кручением, внецентренное растяжение (сжатие), косой изгиб. Теперь давайте перейдем непосредственно к категориям и не забывайте переходить по ссылкам на интересующую вас подкатегории.

Что можно найти в данной категории задач?

• определение реакций в опорах из уравнений равновесия статики;
• расчет ВСФ методом сечений;
• вычисление продольной и поперечной силы;
• расчет изгибающего момента;
• расчет нормальных и касательных напряжений;
• вычисление перемещений поперечных сечений;
• раскрытие статической неопределимости с использованием уравнения совместности деформации.

Растяжение и сжатие

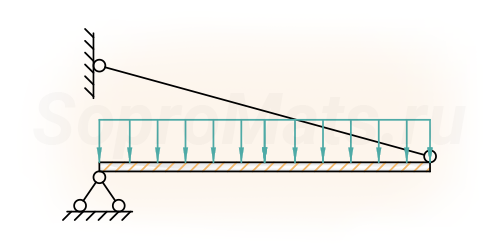
• статически определимые брусья;
• статически неопределимые брусья;
• статически определимые стержневые системы;
• статически неопределимые стержневые системы.

Кручение

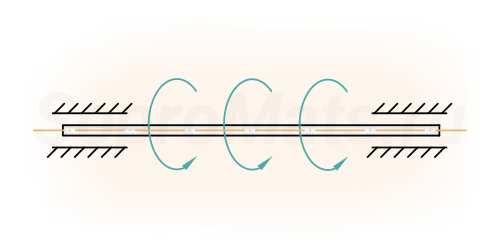
• статически определимое кручение;
• статически неопределимое кручение.

Изгиб

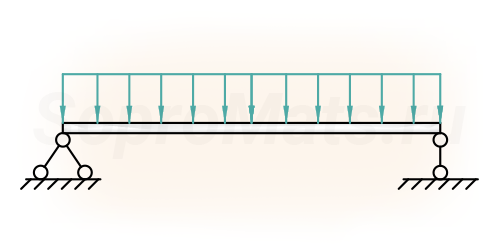
• статически определимый изгиб;
• статически неопределимый изгиб.

Классификация по типу рассчитываемого объекта

В этом разделе все решения распределены по типу рассчитываемого объекта: на балки, рамы, фермы и т. д. Каждая представленная здесь категория имеет укрупненную классификацию, которую можно изучить, перейдя по соответствующим ссылкам.

Балки

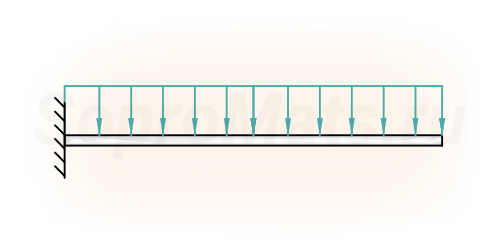
• статически определимые балки;
• статически неопределимые балки.

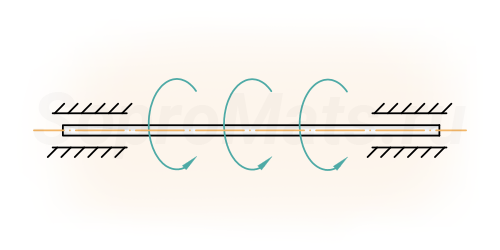
• статически определимые валы;
• статически неопределимые валы.

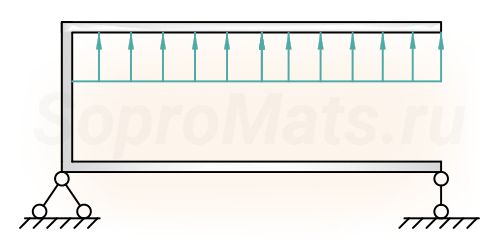
• статически определимые рамы;
• статически неопределимые рамы.

Фермы

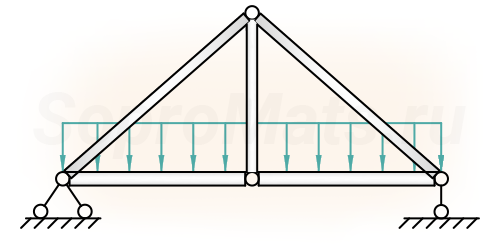
• определение реакций в опорах фермы;
• определение продольных усилий в стержнях методом вырезания узлов, либо методом Риттера.
• построение линий влияния.

Сечения

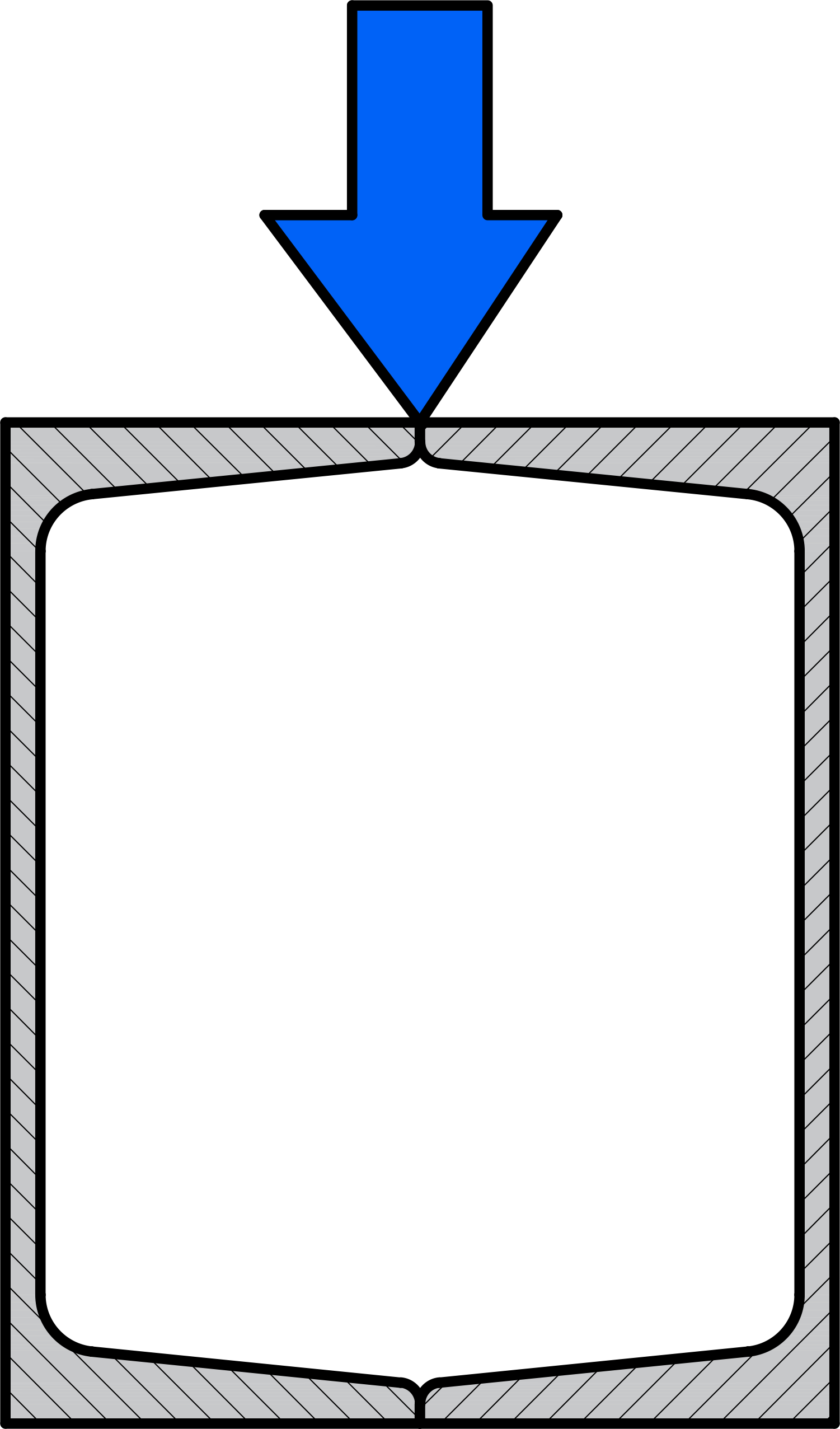
В разделе про сечения, связанные с расчетом геометрических характеристик, принята следующая классификация:

• симметричные и несимметричные сечения, состоящие из геометрических примитивов;
• симметричные и несимметричные сечения, состоящие из металлопрокатных профилей.

Классификация по типу расчета

В этом разделе материалы разделены по типу расчета. Сюда попали расчеты на прочность, жесткость и устойчивость. Здесь же находятся задачи, связанные с расчетом напряжений, эпюр внутренних силовых факторов и другие.

Прочность

В этой категории находятся задачи, связанные с расчетом прочности, при различных видах деформации: изгибе, кручении, растяжении (сжатии) и сложном сопротивлении. Здесь можно встретить как проверочные, так и проектировочные расчета. Найти расчеты на грузоподъемность какой-либо системы.

Жесткость

В расчетах на жесткость, можно найти задачах, в которых исследуются различные элементы конструкций: балки, рамы, валы и другие. Во всех задачах проверяется жесткость, путем сравнения расчетных значений перемещений с допустимыми значениями.

Устойчивость

В примерах на устойчивость, можно найти задачи, связанные с подбором сечения стоек из условия устойчивости, либо расчетом грузоподъемности.

Эпюры

Данная категория, связанна с расчетом эпюр внутренних силовых факторов, при различных видах деформации: растяжении и сжатии, кручении, изгибе и сложном сопротивлении. Есть эпюры, которые откладываются со стороны растянутых волокон (строителям) и сжатых волокон (машиностроителям).

Помощь в решении задач по сопромату на заказ

Это базовые задания, решение которых оказывается под силу почти каждому. Необходимо определить внутренние усилия, возникающие в балке прямоугольного сечения при растяжении её силами, приложенными вдоль оси балки.

Решение производится следующим образом:

1. Разбиваем балку на участки, границами которых являются точки приложения сил либо точки, в которых изменяется площадь поперечного сечения балки.
2. Определяем суммарные усилия на каждом участке, сложив проекции всех сил на ось балки.
3. Определяем нормальные напряжения на участках.
4. Определяем относительные удлинения и перемещения на границах участков если того требует задание.
5. Строим эпюры по полученным данным.

Решение задач по теме «Кручение»

Здесь необходимо определить крутящие моменты и угловые перемещения элементов конструкции, возникающие под действием внешних усилий. В целом подобные задачи аналогичны задачам на растяжение, разница в том что линейные перемещения заменяются угловыми, а роль модуля упругости играет величина, называемая модулем сдвига.

Решение задач по теме «Изгиб»

Задачи на изгиб немного выше предыдущих по сложности, однако, если придерживаться несложных правил, решение окажется быстрым. В заданиях предлагается рассчитать балку на изгиб – определить максимальный изгибающий момент и при известном наибольшем допускаемом напряжении определить площадь её поперечного сечения. alt="изгиб" width="275" height="152" /> alt="изгиб" width="275" height="152" />Вначале необходимо определить тип опор балки (шарнирно-подвижная, шарнирно-неподвижная, консольная заделка) и их количество. Исходя из этого, определяется количество реакций опор, которые необходимо рассчитать.

Далее проводится расчет в следующем порядке:

1. Разбиваем балку на участки, границами которых являются опоры или точки приложения сил.
2. Определяем величину поперечных сил и изгибающих моментов на каждом участке. Для этого составляем уравнения равновесия, приравнивая сначала сумму сил, а затем моментов к нулю и решая получившиеся уравнения. Необходимо руководствоваться следующим правилом: поперечные силы и изгибающие моменты направляются так, чтобы они растягивали нижние волокна балки.
3. Из получившихся величин моментов выбираем максимальный изгибающий момент.
4. Исходя из условия прочности, определяем необходимый момент сопротивления поперечного сечения балки.
5. При заданной форме поперечного сечения определяем его площадь.

Решение задач по теме: «Продольный изгиб»

Продольный изгиб возникает в стержне под действием сжимающих сил, приложенных вдоль его оси. При превышении силой некоего критического значения стержень теряет свою устойчивость. Данное значение и предлагается определить в задачах на устойчивость.

Задача решается следующим образом:

1. Пользуясь заданной формой поперечного сечения стержня, определяем его площадь в относительных величинах, так как абсолютные необходимо найти.
2. Определяем осевые моменты инерции и находим минимальный из них.
3. Пользуясь формулой, с учетом коэффициента приведения длины, находим гибкость стержня.
4. Путем последовательных приближений находим величину поперечного сечения стержня. Для этого задаем первоначальную величину коэффициента формулы φ равной 0,5 и вычисляем величину условной единицы площади и гибкость стержня при этом значении. По найденной величине гибкости λ определяем табличное значение коэффициента φ и вычисляем разницу между вычисленным и табличным значением. Если разница оказывается больше 5%, повторяем вычисления, принимая новое значение φ равным среднему арифметическому между табличным и вычисленным.
5. Повторяем вычисления пока разница не станет меньше 5%. Затем подставляем найденную величину условной единицы площади в формулу и находим площадь поперечного сечения стержня.
6. Находим величину критической силы.

Литература

Платное решение задач по сопромату на заказ

• Сколько стоит работа по решению задач?

Цена складывается из множества факторов, основной из которых это сложность работы.

Да. Цена каждой задачи будет уменьшаться прямо пропорционально увеличению их количества.

Работа будет выполняться в указанные при заказе сроки. По возможности будет сделано раньше.

Решение домашнего задания по сопромату

Задача по сопромату 1

Определить моменты шести заданных сил (рис. 1) относительно точек А, В и С, если Р1=30 н, Р2 = 50 н, Р3 = 25 н, Р4=40 и, Р5 = 35 н, Р6=54 н, АВ=1,2 м, ВС = 0,8 м, =55° и = 35°.

Решение задачи 1—определение моментов шести заданных сил отно­сительно точки А (рис. 1, а).

1. Центр моментов в точке А. Через точку А проходят линии действия трех сил Р1, Р2 и Р5. Зна­чит для этих сил плечи равны нулю. Следовательно,

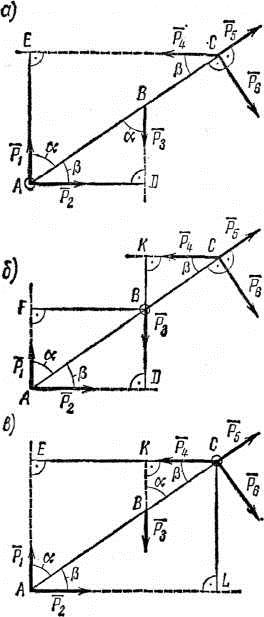
2. Находим момент силы Р3. Опустив из точки А на линию действия Р3 перпендикуляр AD, получим плечо силы Р3. Длину AD легко най­ти, так как это катет треугольника ABD: AD=AB sin a.

3. Величина момента отрицательная (сила Р3 поворачивает плечо AD вок­руг точки А по ходу часовой стрелки), следовательно,

4. Находим момент силы Р4. Плечом силы Р4 является перпендикуляр АЕ к СЕ—линии действия силы Р4. Из тре­угольника АСЕ

Величина момента положительная (плечо АЕ поворачивается около точки А силой Р4 против хода часовой стрел­ки). Следовательно,

5. Находим момент силы Р6. Плечом силы Р6 относительно точ­ки А является отрезок АС, так как сила Р6 направлена к АС перпендикулярно.

Задача по сопромату 2 с решением.

Движение точки А задано уравнениями:

где х и у—в см, a t — в сек. Определить траекторию движения точки, скорость и ускорение в моменты = 0 сек, =1 и = 5 сек, а также путь пройденный точкой за 5 сек.

Решение задачи.

1. Определяем траекторию точки. Умножаем первое заданное уравнение на 3, второе—на (—4), а затем складываем их левые и правые части:

Получилось уравнение первой степени — уравнение прямой ли­нии, значит движение точки — прямолинейное.

Для того чтобы определить координаты Ао — начального поло­жения точки, подставим в данные сравнения значение = 0; из первого уравнения получим = 2 см, а из второго =1 см. Замечая, что при любом другом значении t (так как в оба уравнения t входит во второй степени) координаты х и у движущейся точки только возрастают, делаем окончательный вы­вод: траекторией точки служит полупрямая Зх — Ау — 2 = 0 с началом в точке Ао (2; 1).

2. Определяем скорость движения точки, для чего сначала найдем ее проекции на оси координат:

Таким образом, уравнение скорости имеет вид = 5t.

При = 0 начальная скорость точки = 0.

При = 1 сек. скорость точки = 5 см/сек.

При = 5 сек. скорость точки = 25 см/сек.

3. Определяем ускорение точки.

Проекции ускорения на оси координат:

Как видно, проекции ускорения не зависят от времени, движения, значит ускорение тоже постоянно и

т. е. движение точки равноускоренное.

4.Так как в данном случае движение точки прямолинейное, то модуль ускорения можно определить путем непосредственного дифференцирования уравнения скорости:

5.Как установлено, движение точки прямолинейное, равно­ускоренное, значит векторы скорости и ускорения совпадают с траекторией точки, т. е. направлены вдоль полупрямой Зх — 4у—2 =0.

6.Определяем путь, пройденный точкой за первые 5сек дви­жения. Выразим предварительно путь как функцию времени t.

Проинтегрируем последнее выражение:

но так как в данном случае начальное расстояние = 0, то окон­чательно .

И теперь находим, что за t=5сек точка проходит расстояние

Задача по сопромату 4

Точка движется по траектории, изобра­женной на рис. 1.44, а, согласно уравнению s=0,2 (s —в метрах, t — в секундах). Определить скорость и ускорение точки в положениях 1 и 2.

Решение задачи. Время, необходимое для перемещения точки из положения 0 (начала отсчета) в положение t, опреде­лим из уравнения движения, подставив частные значения расстояния и времени:

Уравнение изменения скорости

Скорость точки в положении 1

Уравнение изменения касательного ускорения

Касательное ускорение точ­ки в положении 1

Нормальное ускорение точки на прямолинейном участке траектории равно нулю. Ско­рость и ускорение точки в конце этого участка траекто­рии показаны на рис. 1.44, б. Определим скорость и уско­рение точки в начале криво­линейного участка траектории. Очевидно, что = 11,5 м/с,

Нормальное ускорение точки в начале криволинейного участка

Скорость и ускорение в начале криволинейного участ­ка показаны на рис. 1.44, в (векторы и изобра­жены без соблюдения масштаба).

Положение 2 движущейся точки определяется прой­денным путем, состоящим из прямолинейного участка 0—1 и дуги окружности 1—2, соответствующей цент­ральному углу 90°:

Время, необходимое для перемещения точки из положения 0 в положение 2,

Скорость точки в положении 2

Касательное ускорение точки в положении 2

Нормальное ускорение точки в положении 2

Ускорение точки в положении 2

Скорость и ускорения точки в положении 2 показаны в (векторы и изображены без соблюде­ния масштаба).

Задача 5 по сопромату

Определить из условия прочности раз­меры площадей сечений чугунного бруса, если допускаемые напряжения для материала бруса

на растяжение [р]=60 Н/мм2, на сжатие [с]=120 Н/мм2.

Решение. Брус представляет собой один раз статиче­ски неопределимую систему, так как для определения двух опорных реакций НА и НB можно составить только одно уравнение равновесия

Из условия деформации бруса следует, что перемеще­ния опорных сечений равны нулю. Отбросим закрепление в точке А и, применив принцип независи­мости действия сил, составим уравнение перемещений учитывая, что сумма перемещений сечения А от всех сил равна нулю:

Выразим перемещения с помощью закона Гука через соответствующие силы:

lнА = НА • 2a/(E - 2F)+HA 2,5a/(EF)=3,5HA a/(EF);

Подставив значения lHA, lP1, 1Р2 в уравнение пере­мещений, получим

3,5HA a/(EF)+3Pi a /(EF) – 2,5P2 a/(EF)=0,

откуда 3,5НА + ЗР1 — 2,5Р2=0.

НА = (2,5Р2 — ЗР1)/3,5=(2,5- 40 — 3- 10)/3,5=20 кН.

Из уравнения равновесия найдем

НВ = Р2 — Р1 — HA = 40 – 10 — 20=10 кН.

Значения реакций НА и НB получились положитель­ными. Следовательно, их направления, которыми мы зада­лись, соответствуют действительным.

Эпюра продольных сил показана на рис. 2.14, в.

Определим нормальные напряжения в поперечных се­чениях каждого участка:

Эпюра нормальных напряжений приведена на рис. 2.14, г. Опасными являются поперечные сечения уча­стка //.

F15- 103/[P]=15- 103/60=250мм2.

Задача К точкам А, С и В, D, об­разующим вершины квадрата со стороной 0,5 м

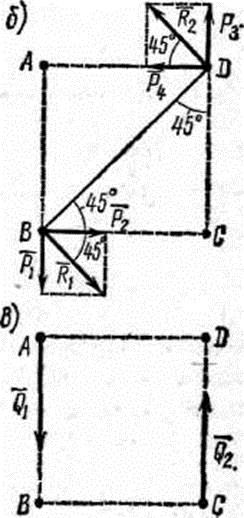
(рис. 66, а), приложены равные по модулю силы (Р=12 н) таким образом, что они образуют две пары сил (P1, P3) и (Р2, Р4). Опре­делить момент равнодействующей пары сил.

Решение 2 задачи

1. Перенесем силы P1 и Р3 из точек А и С соответственно

в точки В и D (рис. 66, б). В точках В и D получаются системы сходящихся сил P1 и Р2; Р3 и Р4 с одинаковыми модулями.

2. Сложим попарно эти силы у каждой из точек В и D. В обоих

случаях R1=R2 =

3.Силы R, модули которых теперь известны, направлены пер­пендикулярно к диагонали BD квадрата. Значит эта диагональ является плечом вновь образовавшейся пары сил (R1, R2), заменя­ющей собой две данные. - 4.Найдем момент пары (R1, R2):

Эту пару в соответствии со вторым решением можно представить в виде пары (R1, R2) с плечом BD (диагональю данного квадрата).

Но можно равнодействующую пару представить и в любом дру­гом виде, например в виде сил Q = 24н, приложенных к двум любым вершинам квадрата ABCD

Сопромат Задача . Движение точки по прямолинейной траектории описывается уравнением

(s – в м, t – в сек).

Определить скорость и ускорение точки в начале движения. В какие моменты времени скорость и ускорение точки равны нулю? Построить графики перемещений скоростей и ускорений для пер­вых пяти секунд движения.

Решение.

1. Продифференцировав данное уравнение движения, получим уравнение скорости

2.Чтобы определить скорость в начале движения, положим в этом уравнении время t = 0 и получим

3.Чтобы определить, в какие моменты времени ско­рость равна нулю, решим уравнение скорости относительно времени t, при­няв в нем = 0:

Таким образом, скорость точки дважды оказывается равной нулю: первый раз через сек., а второй раз через 3 сек после начала дви­жения.

4. Продифференцировав уравнение скорости, получим от уравнение касательного ускорения:

5. Подставив в это урав­нение значение t = 0, найдем, что в начале движения

Получившееся отрицательное значение касательного ускорения при положительном значении указывает на то, что в начале движение было замедленным.

6.Определим, в какой момент времени касательное ускорение равно нулю:

если , то 1,2t —2 = 0.

Отсюда находим, что при t’= сек.

7.Для построения графиков предварительно составим сводную таблицу числовых значений s, v и при значениях t от 0 до 5 сек.

8. Построенные по этим данным графики показаны на рис.. Графики даны в масштабах: по оси времени = 0,1 сек/мм; по оси s: = 0,08 м/мм (на графике перемещений); по оси v: = 0,2 м/сек-мм (на графике скоростей,) и по оси = 0,2 -мм (на графике ускорений).

Рекомендуется построить графики в масштабах: = 0,05 сек/мм, = 0,04 м/мм, = 0,l м/сек-мм и = 0,l -мм и дать по ним описание движения точки.

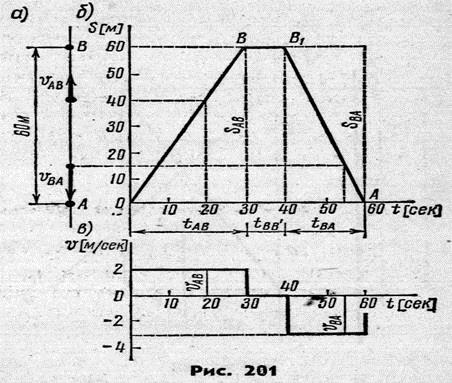
Задача Точка, совершая равномерное и прямолинейное движение, проходит прямолинейный участок траектории АВ, рав­ный 60м (рис. 201, а) за 30сек. Простояв затем 10сек на месте, точка возвращается в исходное положение со скоростью 3 м/сек. Сколько всего времени проходит от начала движения точки до ее возвращения в исходное положение? Какой путь проходит точка?

Построить графики перемещения и скорости точки.

Решение.

1. Расстояние от А до В, равное = 60м, равномерно прой­дено за =30сек. В данном случае начальное расстояние = 0, поэтому из уравнения (б) находим скорость точки на участке АВ

2.Точка находится в покое в течение времени .

3.Точка возвращается в исходное положение, пройдя расстоя­ние от В до А = 60 м со ско­ростью = 3 м/сек за время

4.Время от начала движения до момента возвращения в исход­ное положение равно:

5.Путь, пройденный точкой за это время,

6. Построим теперь график перемещения (рис. 201, б) и ско­рости точки (рис. 201, в) с одина­ковым масштабом по оси времени.

Пример 2.14. Абсолютно жесткая (недеформирующаяся) балка АВ закреплена левым концом при помощи шарнирно неподвижной опоры А; в точках С и D поддерживается двумя вертикальными стержнями, изготовленными из различных материалов: один стальной (Fc=600 мм2), другой медный (FM=300 мм2).

Опреде­лить реакцию опоры А и усилия в стержнях при нагружении правого конца балки силой Р=80 кН. Мо­дули упругости стержней Eс=2,0-105 Н/мм2, Eм=1,0х105Н/мм2.

Решение. Задача статически неопределимая, так как неизвестных сил четыре: составляющие НА и VА – реакции опоры А и усилия в стержнях NM и NC(рис.2,13,б), а статика дает три уравнения равновесия. Составляем уравнение проекций сил на горизонтальную ось

на вертикальную ось

Уравнение моментов сил относительно центра шар­нира А имеет вид:

или после простых преобразований и сокращения

2NM+NC=3P

Уравнение перемещений составим на основе рассмот­рения деформаций системы.

Вследствие удлинения стержней балка АВ поворачи­вается вокруг оси шарнира А. Так как балка абсолютно жесткая, то при ее вращении точки С и D, переместившись в положения С1 и D1 остаются на одной прямой АВ1.

Учитывая, что перемещения при упругих деформа­циях весьма малы, можно считать вертикальные переме­щения точек С и D равными удлинениям стержней lс и lм.

Из подобия треугольников АСС1 и ADD1 получаем

lМ=2 lС.

Выражаем удлинения lс и lм по закону Гука:

Mc=Ncl/(EcFc); MM=NM l/(EMFM).

Таким образом, подставляя значения lс и lм в урав­нение перемещений, получаем

NMl/(EMFM)=2NCl/(ECFC),

NM=2NCEMFM /(ECFC).

Учитывая найденное соотношение, находим

4NCEMFM /(ECFC)+NC=3P,

Определяем теперь величину NM:

Вертикальная составляющая реакции опоры А опре­делится из уравнения равновесия

VA = P – Nc – Nм= – 2Р(ECFC+EMFM)/(ECFC+4EMFM).

Знак минус показывает, что реакция направлена не вверх, как предполагалось вначале , а вниз.

Из этого примера, как и из предыдущего, следует, что распределение усилий между элементами статически неопределимой конструкции в отличие от статически определимых зависит от соотношения жесткостей ее элементов.