Содержание занятий и домашние задания по физике

Главная » Статьи » Содержание занятий и домашние задания по физике

Содержание занятий и домашние задания по физике

I семестр 2015/2016 уч. Год Занятие №91. Семинар по физике «Механические колебания» Контрольные вопросы

Какие процессы называются колебательными? В чём состоят различия колебаний свободных и вынужденных? Приведите примеры.

Составьте дифференциальное уравнение гармонических колебаний пружинного маятника и приведите его решение.

Уравнение гармонического колебания, его график. Сопоставьте все величины, входящие в уравнение, с графиком гармонического колебания.

Составьте дифференциальное уравнение затухающих колебаний пружинного маятника, приведите его решение.

Уравнение свободных затухающих колебаний. График затухающего колебания.

Характеристики затухания: коэффициент трения, коэффициент затухания, логарифмический декремент затухания.

Вынужденные колебания. Явление резонанса. Резонансная кривая.

Литература для подготовки:

Антонов В.Ф., Черныш А.М., Козлова Е.К., Коржуев А.В. Физика и биофизика. ГЭОТАР-Медиа.2010.

Антонов В.Ф., Черныш А.М., Козлова Е.К., Коржуев А.В. Физика и биофизика. Практикум. ГЭОТАР-Медиа.2008.

Задачи для решения на занятии №9 «Механические колебания»

1.Охарактеризуйте процессы, графики которых представлены на рисунках 1-3 (по оси OУ – изменение координаты тела X, по оси ОХ – время t). Для каждого из процессов определите амплитуду, период, линейную и циклическую частоты, запишите закон изменения смещения от времени.

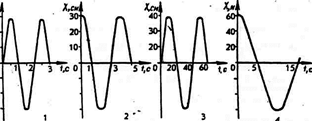
Уравнение движения точки имеет вид м. Найти амплитуду, период и частоту колебаний. Записать законы изменения скорости и ускорения колеблющегося тела.

Используя данные графика (рис. 4) затухающих механических колебаний груза на пружине, найдите значения физических величин, характеризующих данный тип колебаний (по оси OУ – смещение колеблющегося тела s в м, по оси ОХ – время t в секундах):

ν, Гц

ω, с -1

β , с -1

Амплитуда затухающих колебаний уменьшилась за 2 минуты в 4 раза, во сколько раз она уменьшится за 8 минут?

Домашняя работа №9 «Механические колебания»

I.Решите задачи:

Тело массой m движется так, что зависимость пройденного пути от времени описывается уравнением S=Acosωt, где A и ω – постоянные. Запишите закон изменения силы от времени.

Груз подвешен на пружине, совершает свободные гармонические колебания. На графике схематически изобразите процесс изменения смещения груза от времени (относительно положения равновесия):

а) движение началось из положения равновесия

б) груз отвели от положения равновесия вертикально вниз.

С помощью программы Excel на одной координатной плоскости постройте два графика затухающих механических колебаний, осуществляющихся по закону в течение 30 секунд. При этом для обоих колебаний А₀=0,5м, = 1 c -1 , ₁=0,1 с -1 , а ₂=0, 01с -1 .Объясните, как отличаются и от чего зависят скорости затухания амплитуд колебаний, подсчитайте логарифмические декременты исследуемых колебаний.

II. Самоподготовка: Ответить письменно на контрольные вопросы к следующему занятию.

«С. М. КУРАШЕВ ОПТИКА И АТОМНАЯ ФИЗИКА Домашние задания. Методические указания Москва 2011 Сборник задач для домашних заданий по курсу Оптика и атомная физика Кафедра физики . »

Данный материал содержит задачи по волновой оптике и атомной физике, предназначенные для самостоятельного решения при выполнении домашних заданий студентами, слушающими трёх семестровый курс Общей физики. Предусмотрена возможность проверки заданий при помощи системы программированного контроля. В сборнике имеются методические указания к решению задач, приведены примеры решения типичных задач. В приложении содержатся некоторые справочные данные.

МЕТОДИЧЕСКИЕ УКАЗАНИЯ К РЕШЕНИЮ ЗАДАЧ

Примеры решения и оформления задач Задачи для домашнего задания. Оптика и атомная физика Глава 1. Геометрическая оптика Глава 2. Интерференция света Глава 3. Дифракция. Спектральные приборы Глава. 4. Поляризация света Глава 5. Тепловое излучение Глава 6. Теория относительности Глава 7. Квантовые свойства света Глава 8. Атом Бора Глава 9. Состояние электронов в атоме Глава.10. Рентгеновское излучение Приложение. Основные физические величины и единицы их измерения

МЕТОДИЧЕСКИЕ УКАЗАНИЯ К РЕШЕНИЮ ЗАДАЧ

Изучение физики предполагает приобретение навыков решения задач, на которых вырабатывается умение применять основные физические законы к анализу реально протекающих процессов.

Решение задач всегда было необходимым элементом любого курса физики, начиная с элементарного школьного курса и кончая университетским курсом теоретической физики.

Задачи дают студенту первое представление о физическом мире, о его закономерностях, методах его описания и путях познания. Это, так сказать, «пробный камень», на котором изучающий физику должен продемонстрировать уровень познания её основных законов, умения и навыки, приобретенные в процессе обучения, в применении теоретического материала к конкретным, пусть даже и сильно идеализированным ситуациям.

Решение задач есть, в некотором смысле, вид творчества и подчиняется во многом тем же закономерностям, что и работа ученого над научной проблемой или работа инженера в практической деятельности.

Содержание типичной задачи предполагает нахождение одних физических величин через другие, которые известны. Такой подход отражает ситуацию, складывающуюся при проведении исследовательской работы, когда удается измерить одни параметры, характеризующие явление, непосредственно, а другие вычисляются на основании известных закономерностей. При этом в одном случае оказываются известными одни величины, а в другом случае - другие. Поэтому надо уметь подходить к анализу одной и той же задачи с разных сторон, используя известные величины и выражать через них неизвестные. Указанная тенденция отражена в составлении пяти вариантов к каждой задаче.

Нахождение общей формулы, определяющей неизвестную величину через исходные данные, является только первым шагом к решению задачи. Необходимо получить численное значение искомой физической величины, что требует умения использовать единицы измерения, развития навыков приближенных вычислений, когда требуется оценить порядок получаемого результата и точность найденного числового ответа.

Данный сборник заданий и методических указаний содержат два раздела. В первом разделе приведены задачи для самостоятельного решения в процессе выполнения домашнего задания. Второй раздел содержит задачи для решения на семинарских и практических занятиях. Структура задач этих разделов несколько отличается.

Задача для домашнего задания формулируется в общем виде. К ней дается в виде таблицы по пять наборов числовых данных, размещенных в отдельных строках, которые обозначены соответствующими номерами (шифрами). Как правило, величина, числовое значение которой требуется определить в данном шифре, фиксирована знаком "?". В некоторых из задач неизвестная величина указывается в тексте задачи. Величины, обозначенные прочерком "-", для решения данного шифра не требуются, определять их не нужно.

Единицы измерения, в которых необходимо выразить определяемую величину, указаны в заголовке соответствующей графы таблицы числовых данных (столбца). Во многих случаях используются дольные или кратные от единиц системы СИ, а также другие единицы, применяемые в науке и технике. Таблицы единиц измерения физических величин, соотношения между различными единицами, приставки для образования кратных и дольных единиц, а также значения основных физических и астрономических постоянных содержится в Приложении (табл. 1-3).

Задачи, помещенные в данных методических указаниях, сгруппированы по тематическим параграфам, охватывающим все основные разделы физики волновых процессов, оптики и атомной физики, которые входят в программу изучения курса Общей физики в институте. Параграф состоит и шести стилизованных задач, каждая из которых мультиплицирована пятью наборами условий, сгруппированных в виде таблицы.

Задачи предназначены для двух домашних заданий, которые выполняют в течение семестра студенты всех лекционных потоков, изучающих последний (третий) раздел стандартного курса Общей физики – оптику и физику атомных явлений, а также курс «Физика волновых процессов».

Сроки сдачи домашних заданий устанавливаются семестровым графиком учебных занятий, помещенным в учебную книжку студента. Вариант и номера задач, входящих в данный вариант, определяется маршрутом выполнения домашних заданий (составляется лектором потока), так же помещенным в учебную книжку, в соответствии с порядковыми номерами студентов по списку группы. Выбор конкретных условий к данной текстовой задаче (номер шифра) определяется аналогично в соответствии с номером студента по списку согласно таблице:

№ студентов групповому журналу Домашнее задание должно быть оформлено в отдельной тетради, на обложке которой указывается: группа, фамилия, порядковый номер студента по списку группы, номер задания (ДЗ 1, ДЗ 2), номер варианта, номера задач по сборнику, шифр.

Работы, не содержащие указанных данных, приниматься не будут!

При решении каждой задачи помимо ее номера необходимо записать условия и сделать чертеж, поясняющий задачу. На чертеже указать все рассматриваемые объекты, обозначения, векторы, систему координат. В комментариях к рисунку разъяснить роль идеализаций и допущений, сделанных в задаче.

Рекомендуется руководствоваться следующими правилами в процессе решения:

1. Прежде всего, необходимо уяснить условие задачи, если это необходимо, обязательно сделать рисунок, определяющий её суть.

2. Следует обосновать использование применяемых при решении физических законов, дать их математическую запись в одной системе единиц (желательно СИ).

Решить полученную систему уравнений и записать ответ (если возможно) в аналитическом виде.

3. При решении задач студент должен проявить знание общей физики, уметь идеализировать явления, применять законы сохранения, выявлять условия симметрии, проводить выделение безразмерных комбинаций параметров и т.д.

4. За редкими исключениями, каждая задача должна быть решена в общем виде, при этом искомая величина должна быть выражена через заданные в условии величины.

5. Полученное в общем виде решение необходимо проверить с точки зрения размерности в обобщенном (буквенном) смысле. Если размерность не соответствует искомой физической величине, нужно искать ошибки в решении.

6. Во многих случаях полезно исследовать поведение решения при предельных значениях параметров. Например, решая задачу на нахождение горизонтального ускорения бруска массы m, лежащего на абсолютно гладком клине массы M, получаем ответ a Устремим массу М к бесконечности, что физически соответствует гораздо более простой задаче с закреплённым клином В предельном случае мы получили ответ, совпадающий со стандартным результатом физически тривиальной задачи. Отсюда делаем вывод о разумности полученного ответа.

7. Убедившись в правильности решения в общем виде, подставляют в него численные данные, при этом их предварительно выражают в единицах одной системы (например, СИ или СГС). Необходимо так же проследить, чтобы используемые формулы соответствовали применяемой системе единиц. Например, вычисляя силу электростатического взаимодействия зарядов, мы должны четко определить систему единиц 8. Получив результат, необходимо указать размерность единицы измерения искомой величины в той системе единиц, в которой производилось вычисление. Провести проверку размерности результата, а также дать анализ полученного ответа. Затем, если нужно, выразить ответ в тех единицах, которые указаны в заголовке соответствующей графы таблицы числовых данных.

9. Необходимо помнить, что числовые значения физических величин всегда приближенные. Поэтому при выполнении расчетов надо руководствоваться правилами действий с приближенными числами. Например, если сомножители содержат по значащих цифры, то и произведение должно содержать только 3 значащих цифры, остальные цифры должны быть отброшены. Напомним, что значащими цифрами называются все цифры в десятичном изображении числа, кроме нулей, стоящих в начале числа. Например, в числе 0,0350 первые два нуля не являются значащими. Их назначение – установление десятичных разрядов остальных цифр. В то же время, нуль после цифры является значащей цифрой.

10. Вычисление следует проводить так, чтобы окончательный результат имел погрешность, не превышающую пять процентов, при этом ответ следует выразить в тех единицах, которые указаны в заголовке соответствующей графы (столбца) таблицы числовых данных.

11. Если при решении задачи возникают осложнения с пониманием условии задачи и, как следствие, с конкретным способом её решения, необходимо внимательно ознакомиться с рекомендованной литературой, а именно: с теми разделами курса, которые нашли отражение в условиях. В случае неудачи рекомендуется обратиться за помощью к преподавателю.

Задача № 1 (шифры 1, 2, 3) На плоскую дифференциальную решетку, содержащую |N| штрихов, нормально падает приходящееся на 1 мм длины, равно /n/. Максимальный порядок спектра, который можно получить в данной области спектра - /m/, минимальное расстояние между спектральными линиями, которые способна разрешить решетка в этой области спектра - / /. Спектр порядка /m/ фотографируется на фотопластинке с помощью объектива с фокусным расстоянием /f/, при этом на фотопластинке между спектральными линиями / / и / 0 / получается расстояние / /. Определить неизвестную величину.

1) Шифр 1. Необходимо определить максимальный порядок спектра, найдем период решетки.

Выразим его в нанометрах: d = 2000 нм.

При нормальном падении монохроматического света на дифракционную решетку положение главного максимума m – ого порядка определяется уравнением:

Не все натуральные значения m, входящие в это выражение, допустимы. Так как sin 1, то на m должно быть наложено ограничение Учитывая это обстоятельство, получим И, так как m должно быть целым, находим, что максимальным порядком спектра будет 3.

Этот ответ заносится на карту. Отметим, что общее число штрихов N при решении задачи нам не понадобилось. Это условие оказалось лишним.

«МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ ГОУ ВПО СИБИРСКАЯ ГОСУДАРСТВЕННАЯ ГЕОДЕЗИЧЕСКАЯ АКАДЕМИЯ Л.Д. Дикусар, И.Г. Баранник ПОСОБИЕ ДЛЯ ПОДГОТОВКИ К ИНТЕРНЕТ-ЭКЗАМЕНУ ПО ФИЗИКЕ Утверждено Редакционно-издательским советом академии в качестве учебного пособия Новосибирск СГГА 116 2009 УДК 53 (О75) Д 45 Рецензенты: Академик академии естествознания, доктор физико-математических наук, профессор Новосибирского государственного университета экономики и управления Т.Я. Дубнищева Кандидат. »

«МИНИСТЕРСТВО СЕЛЬСКОГО ХОЗЯЙСТВА РОССИЙСКОЙ ФЕДЕРАЦИИ ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ АЛТАЙСКИЙ ГОСУДАРСТВЕННЫЙ АГРАРНЫЙ УНИВЕРСИТЕТ Л.А. Беховых, С.В. Макарычев, И.В. Шорина ОСНОВЫ ГИДРОФИЗИКИ Учебное пособие Рекомендовано Учебно-методическим советом по почвоведению при УМО по классическому университетскому образованию в качестве учебного пособия для студентов высших учебных заведений, обучающихся по специальности и направлению. »

«Новосибирский государственный аграрный университет Инженерный институт Физика Элементы физики твёрдого тела Учебное пособие Новосибирск 2012 УДК 539.21 (075) ББК 22.37, Я 73 Э 456 Кафедра теоретической и прикладной физики Составители: канд. техн. наук, доц. В.Я. Чечуев; канд. техн. наук, доц. С.В. Викулов; доц. И.М. Дзю Рецензенты: д-р физ.-мат. наук, проф. М.П. Синюков, НГАВТ; канд. физ.-мат. наук, доцент В.И. Сигимов, НГАВТ Элементы физики твёрдого тела: учеб. пособие / Новосиб. гос. аграр. »

«СТОЛЯРОВ А.А., АНДРЕЕВ В.В. МЕТОДИЧЕСКИЕ УКАЗАНИЯ по организации и проведению итоговой государственной аттестации бакалавров и магистров по профилю подготовки Наноинженерия Под редакцией заслуженного деятеля науки РФ, Член-корреспондента РАН, профессора, В.А.Шахнова Комплект учебно-методического обеспечения для подготовки бакалавров и магистров по программам высшего профессионального образования направления подготовки Нанотехнология с профилем подготовки Наноинженерия Москва МГТУ им.Н.Э.Баумана. »

«Федеральное агентство по образованию Государственное образовательное учреждение высшего профессионального образования ТОМСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ С.И. Кузнецов КОЛЕБАНИЯ И ВОЛНЫ. ГЕОМЕТРИЧЕСКАЯ И ВОЛНОВАЯ ОПТИКА Учебное пособие 2-е издание, переработанное, дополненное Издательство Томского политехнического университета 2007 УДК 530 К 89 Кузнецов С. И. К 89 Колебания и волны. Геометрическая и волновая оптика: учебное пособие. – Томск: Изд-во Томского политехнического университета, 2007. »

«МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ САНКТ-ПЕТЕРБУРГСКИЙ НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ УНИВЕРСИТЕТ ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ, МЕХАНИКИ И ОПТИКИ Г.Н. Дульнев ТЕОРИЯ ТЕПЛО- И МАССООБМЕНА Учебное пособие Санкт-Петербург 2012 Дульнев Геннадий Николаевич, Теория тепло- и массообмена. – СПб: НИУ ИТМО, 2012. – 195 с. В первых главах книги даны выводы уравнений переноса (непрерывности, энергии, движения); изложена теория подобия и построенные на её основе критериальные уравнения. Дан. »

«Министерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования Пермский национальный исследовательский политехнический университет Ю.А. Барков, О.М. Зверев, А.В. Перминов СБОРНИК ЗАДАЧ ПО ОБЩЕЙ ФИЗИКЕ Утверждено Редакционно-издательским советом университета Издательство Пермского национального исследовательского политехнического университета 2011 УДК 530.1(076) Б25 Рецензенты: доктор. »

«Министерство образования и науки Российской Федерации Нижегородский государственный университет им. Н. И. Лобачевского Национальный исследовательский университет С. М. Грач ВЗАИМОДЕЙСТВИЕ МОЩНЫХ РАДИОВОЛН С ИОНОСФЕРОЙ Часть 1. Возбуждение плазменной турбулентности в верхней ионосфере Учебное пособие Рекомендовано методической комиссией радиофизического факультета для студентов ННГУ, специализирующихся по направлению подготовки 010800 Радиофизика. Нижний Новгород 2012 УДК 533.95 ББК В333.475. »

«Министерство образования Республики Беларусь Международный государственный экологический университет им. А.Д. Сахарова Факультет экологической медицины Кафедра биохимии и биофизики ФИЗИКО-ХИМИЧЕСКИЕ МЕТОДЫ АНАЛИЗА Методическое пособие по дисциплине Аналитическая химия для студентов экологических и химико-технологических специальностей Минск МГЭУ им. А.Д. Сахарова 2005 УДК 543.2 Авторы-составители: д.х.н., профессор Баев А.К.; к.х.н., ст. преп. Свирко Л.К.; к.х.н., Копылович М.Н. Под общей. »

«Н. П. Белов, О. К. Покопцева, А. Д. Яськов ОСНОВЫ КРИСТАЛЛОГРАФИИ И КРИСТАЛЛОФИЗИКИ ЧАСТЬ I ВВЕДЕНИЕ В ТЕОРИЮ СИММЕТРИИ КРИСТАЛЛОВ Учебное пособие Санкт-Петербург 2009 МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ, МЕХАНИКИ И ОПТИКИ Н. П. Белов, О. К. Покопцева, А. Д. Яськов ОСНОВЫ КРИСТАЛЛОГРАФИИ И КРИСТАЛЛОФИЗИКИ ЧАСТЬ. »

Материалы этого сайта размещены для ознакомления, все права принадлежат их авторам.
Если Вы не согласны с тем, что Ваш материал размещён на этом сайте, пожалуйста, напишите нам, мы в течении 1-2 рабочих дней удалим его.

Семинар - Физический факультет - 04.12.2015

Решение задач по физике в средней школе – важный этап становления будущего специалиста в области естественных и технических наук. К сожалению, сокращение часов на изучение физики в школе привело к тому, что часть выпускников имеет размытое представление о физической науке, и уж, тем более, не умеет решать задачи. Работы ведущих преподавателей физического факультета МГУ сформировали систему решения школьных физических задач, основанную на пошаговых алгоритмах. Предлагаемые алгоритмы, их пошаговое содержание, методология их применения, связь с моделированием и олимпиадными задачами обсуждались в рамках семинара 04.12.15.

На семинар прибыло 23 учителя физики, в том числе 4 участника не проходили электронную регистрацию. Учителя приняли живое участие в дискуссии по предлагаемой теме, активно задавали вопросы выступающим, вносили предложения по содержанию рассмотренных алгоритмов.

Участники семинара по его окончании получили сертификат.

Краткие аннотации выступлений

Алгоритмический подход при решении задач динамики
П.Ю. Боков

Рассмотрен алгоритмический подход решения задач динамики как с применением законов Ньютона, так и с применением законов сохранения импульса и механической энергии. Показаны важность выбора моделей, роль системы отсчета на начальном этапе решения задачи, а также, актуальность анализа ответа не только с точки зрения размерности, но и с точки зрения соответствия действительности.

Решение задач отборочного тура олимпиады «Ломоносов-2015» с применением алгоритмов
А.В. Грачев

Предложен вариант решения двух задач динамики, предлагавшихся на отборочном туре олимпиады «Ломоносов-2015» по физике. Рассмотрена важность последовательности действий при решении задач.

Алгоритмизация задач механики и их решение с помощью вычислительных средств
Е.А. Михайлов

Алгоритмизация – важный этап написания компьютерной программы. Большая часть задач механики, не имеющих аналитического решения в рамках школьного курса физики и математики, современными школьниками может быть решена путем численного моделирования с использованием распространенных программных продуктов, например, таких как Microsoft Excel. В сообщении рассмотрен один из подходов к решению задач с применением вычислительных средств.

Регистрация на семинар начнется в 17.30. Одна из основных трудностей при освоении школьниками курса физики связанна с решением задач. Причем речь идет не только об олимпиадных задачах, речь, в том числе, о задачах, встречающихся в заданиях ГИА. В рамках семинара авторским коллективом нового УМК по физике (авт. Грачев А.В., Погожев В.А. и др.) предлагается рассмотреть варианты типизации школьных задач по физике и пошаговый подход к их решению.

Задания дви мгу по физике. Что такое ДВИ? или Как поступают в МГУ? Общая информация о ДВИ по истории

Один из самых известных и престижных вузов нашей страны с достаточно высоким конкурсом на бюджетные места. Вступительные экзамены по различным предметам предусмотрены практически на всех факультетах. Но обычно больше всего вопросов вызывает у абитуриентов ДВИ по математике - ведь этот экзамен сдается при поступлении на 16 из 84 программ МГУ для очного бакалавриата и специалитета.

Избежать ДВИ поможет успешное участие в олимпиадах по математике. Например, победа во всероссийской или вузовской олимпиаде гарантирует БВИ (поступление без вступительных испытаний), а призовое место дает 100 баллов ДВИ, то есть гарантирует поступление даже при «среднем» балле ЕГЭ.

ДВИ по математике в МГУ обычно проводится в середине июля

Из каких заданий состоит ДВИ по математике в МГУ?

Темы и количество заданий, которые будут предложены абитуриентам в рамках ДВИ, остаются неизвестными до самого начала экзамена. Однако в последние годы предлагались задачи, приблизительно схожие по тематике. Это позволяет предположить, что аналогичные задания будут и в 2018 году.

Всего в последние годы экзамен состоит из восьми заданий. С первыми тремя из них способен справиться выпускник школы с твердой четверкой по математике, четвертое задание предполагает наличие более глубоких знаний. В пятом и шестом задании есть «изюминки» - они требуют развитых математических способностей. Седьмое и восьмое задания относятся к уровню повышенной сложности. По статистике, их пытаются решить не более 2 % абитуриентов, а к правильному решению хотя бы одного задания приходит лишь четверть от этого количества.

Приблизительная тематика заданий ДВИ по математике:

1 - на арифметические вычисления;
2 - на квадратные уравнения;
3-4 - на логарифмы и тригонометрические неравенства;
5 - по геометрии (планиметрии);
6 - текстовая задача;
7-8 - стереометрия.

Критерии оценки ДВИ по математике в МГУ

Максимальная оценка, которую можно получить по ДВИ - 100 баллов. При этом критерии их начисления от года к году разнятся, в зависимости от общего количества поступающих и того, как абитуриенты в целом справились с работой. После проверки всех работ собирается статистика, после чего принимается решение о градации технических баллов за задания экзаменационных работ по 100-балльной шкале.

Наибольший удельный вес имеют правильно решенные задачи. Задания, решенные с недочетами (например, если ход решения правильный, но в расчеты закралась ошибка) могут принести половину или треть балла. При этом баллы за частично решенные задачи не суммируются (то есть если у вас два решения по 0,5 балла каждое, к общему количеству технических баллов будет прибавлено 0,5, а не 1).

Обычно 100 баллов можно получить, правильно решив 7 заданий, а в некоторые годы максимальный балл приносило даже решение 6 задач. Для получения минимального положительного балла необходимо набрать 35 баллов (правильно решить одну задачу и показать прогресс в другой). Для большинства технических факультетов, при хорошо сданном ЕГЭ, гарантированное поступление дает результат ДВИ 75-80 баллов. Заметим, что на эту оценку пишут экзамен не более 5 % от общего количества абитуриентов.

В 2017 году соответствие технических баллов и оценок выглядело так:

ДВИ по математике в МГУ сдается в письменном виде

На какие факультеты необходимо сдавать ДВИ по математике в МГУ?

ДВИ необходимо для поступления на технические и математические факультеты, а также ряд специальностей естественно-научных или даже гуманитарных направлений.

Программы очного бакалавриата, на которые необходимо сдавать ДВИ по математике МГУ в 2018 году:

Подготовка к ДВИ МГУ по математике. Насколько всё серьезно?

Ответ на этот вопрос зависит от многих факторов:

От общего уровня подготовки по математике. Например, в вариантах ДВИ МГУ по математике за последние годы почти всегда имелись задания по геометрии и стереометрии, которые сейчас преподаются в школе достаточно слабо. Если ваша школа не имеет физико-математической специализации, «подтягивать» математику нужно начинать заранее.
От результатов ЕГЭ. Баллы ЕГЭ профильных предметов суммируются с результатами ДВИ, что и дает итоговый проходной балл. Например, в 2017 году проходной балл на специальность 01.05.01 Фундаментальная математика и механика МГУ составлял 333 балла. Таким образом, если по трем предметам ЕГЭ (математика, русский язык, физика) абитуриент суммарно получал 270 и более баллов, то для поступления ему было необходимо получить на ДВИ всего 55-65 баллов. Для этого было достаточно решить 4-5 заданий из восьми, то есть для прохождения экзамена не требовалась глубокая специальная подготовка. Если же абитуриент получал по результатам ЕГЭ 250 баллов, то ему нужно было решить правильно 6-7 заданий, а для этого уже были необходимы усиленные занятия.
От выбранного факультета. Удельная доля баллов ДВИ в проходном балле на различные отделения может разниться. Например, для поступления на почвоведение обычно достаточно решить первые три наиболее простые задания ДВИ. Для поступления на отделение «Менеджмент» факультета социологии необходимо получить по ДВИ хотя бы 35 баллов, то есть не написать его на двойку (1-2 задания). На мехмате и ВМК предъявляются гораздо более серьезные требования. Однако абитуриент имеет право подавать документы на три различных направления - то есть, не дотянув по баллам до ВМК, можно пройти на мехмат.

Подготовку к ДВИ по математике в МГУ лучше начинать заранее

Как готовиться?

Если выпускник обладает достаточной усидчивостью и целеустремленностью, подготовиться к ДВИ он вполне может самостоятельно. Сегодня в продаже имеется немало пособий с задачами, приблизительно аналогичными тем, что приходится решать во время вступительных испытаний. С заданиями ДВИ за прошлые годы можно познакомиться на сайте мехмата и Центральной приемной комиссии МГУ.

Для подготовки к ДВИ также можно нанять репетитора или пойти на курсы при интересующем вас факультете. Последний вариант может оказаться более предпочтительным, поскольку преподаватели курсов обычно участвуют в разработке заданий для ДВИ и проверке экзаменов, поэтому хорошо представляют, какие навыки и знания необходимы абитуриентам для поступления. В зависимости от факультета и отделения, начинать посещать курсы рекомендуется за год или даже за два до поступления.

Подготовительные отделения некоторых факультетов позволяют учащимся пройти пробный экзамен, максимально приближенный к реальным условиям и заданиям ДВИ МГУ с последующим разбором примеров и решений. Например, такая возможность на платной основе предлагается Школой молодого предпринимателя при экономическом факультете МГУ.

Дополнительный экзамен по математике является серьезным испытанием для абитуриента не только из-за сложности заданий, но и из-за непривычной обстановки и большого стресса, который может помешать сосредоточиться и правильно решить задачи. Если вы боитесь неудачи, в особом разделе нашего сайта вы можете выбрать вуз и техническую специализацию, куда не нужно сдавать ДВИ по математике. Если вы все же нацелены на МГУ и другие самые престижные вузы, рекомендуем почитать нашу статью «Как поступить в вуз мечты: 9 этапов достижения цели» . Желаем успеха!

Абитуриенты исторического факультета, поступающие для обучения на направление "История", проходят письменное дополнительное вступительное испытание (ДВИ), а поступающие на направление "История искусств" - вступительное испытание творческой направленности, состоящее из письменной и устной части.

Cроки проведения вступительных испытаний для поступающих на исторический факультет МГУ объявляются после начала работы приемной комиссии и указываются в "Календаре абитуриента " и на сайте Центральной приемной комиссии МГУ .

Формы проведения дополнительного вступительного испытания и вступительного испытания творческой направленности устанавливается Центральной приемной комиссией МГУ и становятся известными в день проведения вступительных испытаний.

Результаты этих вступительных испытаний суммируются с баллами по ЕГЭ и баллами за индивидуальные достижения. Итоговое значение составляют общий балл, на основании которого абитуриент участвует в конкурсе.

Дополнительное вступительное испытание (ДВИ) по истории проводится в МГУ централизованно - в один и тот же день для абитуриентов всех факультетов.

Каждый из факультетов МГУ организует на своей площадке ДВИ для тех абитуриентов, у которых данный факультет является базовым. Базовым является тот факультет МГУ, на который абитуриент подал документы первым по времени среди всех факультетов с одним и тем же ДВИ.

Консультация перед ДВИ проводится в предыдущий день в 16:00 для абитуриентов всех факультетов в аудиториях Шуваловского корпуса МГУ .

Результаты оцениваются по 100-балльной шкале и засчитываются на всех факультетах МГУ, на которых в качестве ДВИ сдается история в виде письменного экзамена.

В день проведения экзамена абитуриентам исторического факультета следует заблаговременно (не позднее, чем за час до начала экзамена) собраться перед центральным входом в Шуваловский корпус (Ломоносовский проспект, д.27, к.4).

Начало экзамена - в 10:00 . Продолжительность экзамена - 4 астрономических часа (240 минут) .

Абитуриентам, подававшим заявление по почте, необходимо заранее (как минимум, за день-два до экзамена) получить в приемной комиссии исторического факультета пропуск на экзамен.

Распределение абитуриентов по аудиториям осуществляют сотрудники приемной комиссии. Абитуриенты, опоздавшие к началу экзамена, в аудиторию не допускаются.

паспорт,

несколько ручек синего или черного цвета (следует внимательно отнестись к тому, чтобы вся работа была написана одинаковыми чернилами),

Выходить в туалет можно только в сопровождении сотрудника приемной комиссии, не ранее чем через час после начала экзамена и не позднее чем за час до его окончания.

В день проведения экзамена родители в корпус не допускаются.

Порядок проведения
устной части дополнительного вступительного испытания
творческой направленности
для поступающих на направление "История искусств "

Абитуриенты направления "История искусств" сдают устную часть дополнительного вступительного испытания творческой направленности в аудитории на 6 этаже Шуваловского корпуса МГУ . Начало экзамена - в 10:00.

В день проведения экзамена абитуриентам следует заблаговременно (не позднее, чем в 9:30) собраться перед центральным входом в Шуваловский корпус (Ломоносовский проспект, д.27, к.4).

Лица, не явившиеся на экзамен по уважительной причине (болезнь или иные обстоятельства, подтвержденные документально), допускаются к его сдаче в резервный день.

Сотрудники приемной комиссии сначала собирают абитуриентов в аудиторию для ожидания очереди на экзамен, а затем, по мере завершения ответов ранее пришедших абитуриентов, сопровождают их в экзаменационную аудиторию.

Для участия в экзамене необходимо иметь при себе следующие документы:

паспорт,
пропуск, выданный при подаче документов.

Помимо названных документов абитуриенты могут принести с собой в экзаменационную аудиторию следующие предметы:

ручку синего или черного цвета для заполнения "Листа устного ответа",
минеральную негазированную воду в прозрачной пластиковой бутылке объемом не более 0,6 л.

Категорически запрещается нахождение в аудитории с сотовыми телефонами, карманными компьютерами, электронными словарями, коммуникационными устройствами и иным радиоэлектронным оборудованием, даже если это оборудование находится в выключенном состоянии. В случае нарушения абитуриентом этого правила он удаляется из экзаменационной аудитории.

Во время экзамена от абитуриента требуется дать устный ответ на один вопрос по истории искусства, указанный в выбранном билете и сопровождающем его конверте с иллюстративным материалом. После предварительной подготовки с использованием "Листа устного ответа" абитуриент демонстрирует свои знания членам экзаменационной комиссии под видеозапись, ведущуюся в аудитории.

Максимальная оценка устной части вступительного испытания творческой направленности составляет 30 баллов. Полученный балл суммируется с оценкой за письменную часть (максимально -70 баллов), и на этом основании выставляется общая итоговая оценка на за вступительное испытание в целом (максимальная оценка - 100 баллов).

Объявление результатов и минимальный балл

Даты и время объявления результатов и показа письменных работ сообщаются абитуриентам в аудитории при проведении вступительных испытаний, а также публикуются в "Календаре абитуриента " на сайте исторического факультета.

Минимальное количество баллов, подтверждающее успешное прохождение проводимых МГУ вступительных испытаний и вступительных испытаний творческой направленности устанавливается на уровне минимального количества баллов, необходимого для поступления на обучение по программам бакалавриата и установленного федеральным органом исполнительной власти, осуществляющим функции по контролю и надзору в сфере образования.

Многие знают, что для поступления в МГУ обычных баллов ЕГЭ недостаточно. Здесь мы поговорим о том, что такое «ДВИ» или «дополнительные вступительные испытания». Такие испытания проходят по различным предметам. Нас интересует, конечно, математика.

В качестве ДВИ её сдают при поступлении на 17 из 64 направлений МГУ. Это механико-математический факультет, факультет вычислительной математики и кибернетики, геологический факультет, факультет наук о материалах, экономический факультет, факультет биоинженерии и биоинформатики, направление «Прикладная математика и физика» на факультете фундаментальной физико-химической инженерии, направление «Экономика» Высшей школы государственного аудита, «Менеджмент» Высшей школы современных социальных наук, все направления, кроме «Политологии» факультета государственного управления, а также Высшая школа бизнеса и Московская школа экономики.

За 4 часа абитуриенты должны решить несколько заданий. В последние годы это обычно восемь задач, первые четыре из которых являются более лёгкими, а последние четыре – весьма сложными, представляющими значительную трудность даже для выпускников спецшкол, по этим задачам идёт конкурс на математические направления. Результаты экзамена оцениваются в 100-балльной шкале. Причём 100 баллов может ставиться не только за все 8, но и за 7 (а в некоторые годы ставилось и за 6) правильно решенных задач. Это связано с тем, что все 8 задач решают исключительно редко, на это обычно способны лишь единицы среди тысяч абитуриентов, этих единиц можно смело назвать уникумами.

Чтобы при достаточно высоких результатах ЕГЭ гарантированно поступить на бюджетные места большинства из названных факультетов, надо написать ДВИ на 75-80 баллов.

Среди всех абитуриентов МГУ дополнительный вступительный экзамен по математике сдавали 3732 человека. Из них: на «2» сдали 340 человек, на «30» - 125, на «35» - 154, «40» - 125, на «45» - 134, на «50» - 436, на «55» - 456, «60» - 801, «65» - 572, «70» - 222, «75» - 105, «80» - 85, «85» - 89, «90» - 46, «95» - 30, «100» - 12.

Т.е. мы видим, что только 10-15% абитуриентов, имеющих высокие баллы за ЕГЭ, написав ДВИ по математике, без сомнения, имели реальные шансы поступить на бюджетные места, причём на 80 и более баллов написали математику лишь 7% абитуриентов (на максимальный балл – 0,3%).

Результаты ДВИ МГУ по математике

Теперь рассмотрим результаты ДВИ среди абитуриентов факультета вычислительной математики и кибернетики (ВМК). На этот престижный факультет идут люди исключительно после специальной математической подготовки (учёбы в спецшколах, занятий на курсах и с репетиторами).

Среди поступающих на ВМК МГУ было 128 человек, получивших высший балл по результатам олимпиад, а среди тех 751, кто писал ДВИ при поступлении, результаты следующие:

«2»-17, «30» - 5, «35» - 9, «40» - 9, «45» - 11, «50» - 47, «55» - 74, «60» - 166, «65» - 184, «70» - 73, «75» - 45, «80» - 36, «85» - 35, «90» - 16, «95» - 16, «100» - 8 (т.е. мы видим, что две трети абитуриентов, написавших ДВИ на 100 баллов, подавали документы именно на ВМК).

Таким образом, среди особо подготовленных абитуриентов процент реально претендующих на бюджет оказывается лишь немногим выше: 15-20% (причём 70-75 баллов могут позволить себе только ребята с великолепно сданным ЕГЭ, ведь проходной балл на ВМК очень высокий). И даже среди такой элиты – лишь 1% сдавших ДВИ на максимальный балл.

Результаты ДВИ факультета ВМК МГУ по математике

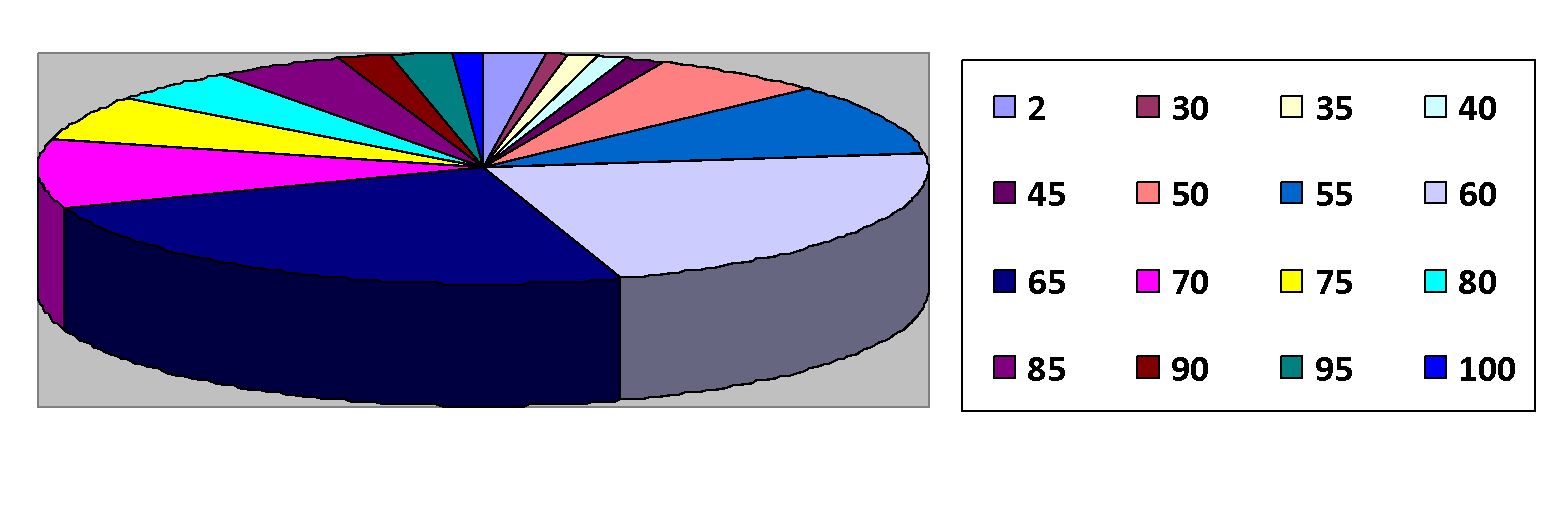
Итак, мы видим, что сдать ДВИ по математике в МГУ оказывается не так уж просто, и к нему требуется особая подготовка.

Многие из выпускников «Математушки» поступили на выбранные факультеты МГУ по результатам олимпиад (победы на «Ломоносове», олимпиаде «Покори Воробьевы горы» и других математических соревнованиях среди обучавшихся в «Математушке» не редкость).

Однако некоторые из выпускников все-таки сдавали дополнительные вступительные испытания и выглядели на них более чем достойно. Возьмём результаты последних лет, когда уже было введено ЕГЭ и ДВИ стали проходить по одному предмету по существующей сейчас схеме.

В этом году новые старшеклассники готовятся покорять «математические горизонты».

Погода в Санкт-Петербурге | Pogoda78.ru